Ici, tout tourne autour du cercle : définitions, formules et calculs du rayon, du diamètre, de la circonférence et de la surface du cercle avec différentes unités de taille sont présentés. Grâce au calculateur de cercle, vous pouvez calculer les propriétés les plus importantes d'un cercle, à savoir le rayon, le diamètre, la circonférence et l'aire d'un cercle. Dans les textes d'aide du calculateur de cercle, chaque conversion pour les propriétés de cercle individuelles est dérivée en utilisant la formule de cercle appropriée.
Contenu sur le thème "Cercle"
Contenu
- Définition d'un cercle
- Calculer le cercle : formules
- Sélectionnez le bouton "Aide"
- Rayon d'un cercle - définition et formule
- Diamètre du cercle - définition et formule
- Périmètre d'un cercle - définition et formule
- Aire d'un cercle - définition et formule
- Exemples de calcul de cercle
- Calculer le rayon d'un cercle
- Calculer le diamètre d'un cercle
- Calculer la circonférence d'un cercle
- Calculer l'aire du cercle
Quel est le nombre Pi ?
En relation avec les calculs et les formules pour le cercle et le calcul des cercles, nous rencontrons à plusieurs reprises Pi ou la lettre grecque π. Le nombre de cercle Pi correspond, quelle que soit la taille d'un cercle, au rapport exact de la circonférence du cercle au diamètre. Pi a un nombre infini de décimales et commence par 3,1415926. La circonférence d'un cercle est donc toujours environ 3,14 fois plus grande que son diamètre.
Unité de taille
Sélectionnez ici l'unité de taille appropriée afin de l'afficher pour les champs de saisie individuels. Vous pouvez sélectionner mm, cm, dm, m, km, in, ft, yd ou mi.
AEt voici comment fonctionne le calculateur : vous pouvez remplir n'importe quel champ de saisie ci-dessous. Les valeurs restantes sont ensuite calculées et renseignées automatiquement à l'aide de la formule de calcul du cercle. Les textes d'aide pour le rayon, le diamètre, la circonférence et l'aire contiennent toujours la dérivation actuelle du calcul actuel. Dès que vous modifiez à nouveau l'une des valeurs, un nouveau calcul des valeurs restantes et une mise à jour des textes d'aide pour la dérivation du nouveau calcul sont effectués.
Rayon
Veuillez saisir le rayon pour calculer le diamètre, la circonférence et l'aire du cercle. Les "textes d'aide" des propriétés de cercle calculées seront mis à jour pour inclure la formule de cercle correspondante ainsi que la dérivation du calcul à partir du rayon saisi vers la propriété respective..
Diamètre
Veuillez saisir le diamètre pour calculer le rayon, la circonférence et l'aire du cercle. Les textes d'aide des propriétés de cercle calculées sont ensuite mis à jour, qui contiennent la formule de calcul associée ainsi que la dérivation de calcul du diamètre saisi vers la propriété respective.
Circonférence
Veuillez saisir la circonférence pour calculer le rayon, le diamètre et l'aire du cercle. Les textes d'aide des propriétés de cercle calculées sont mis à jour et chacun contient une dérivation concrète du calcul en cours, c'est-à-dire de la circonférence au rayon, au diamètre ou à l'aire du cercle.
Aire
Veuillez saisir une aire pour calculer le rayon, le diamètre et la circonférence du cercle. De même, lors du calcul du rayon, du diamètre et de la circonférence, les textes d'aide sont mis à jour afin que la dérivation de la conversion dans chaque cas puisse être comprise.
Schéma
Le schéma vous montre la propriété du cercle sélectionné. Cela vous donne une idée de la façon dont le rayon, le diamètre, la circonférence et l'aire du cercle sont définis. L'affichage change dès que vous cliquez sur un champ "saisie" pour les propriétés du cercle ou sélectionnez un bouton d'aide correspondant.
Définition du rayon
Le rayon r ou rayon est la distance entre le point central M d'un cercle et la ligne du cercle.
Définition du diamètre du cercle
Le diamètre d'un cercle d ou ⌀ est la longueur de la distance de connexion de deux points de la ligne circulaire passant par le centre du cercle M.
Le diamètre est donc la plus grande distance possible entre deux points de la ligne circulaire.
Formule pour le diamètre d'un cercle
Le diamètre d correspond au double du rayon r
d = 2 × r
Définition de la circonférence
La circonférence C est la longueur de la ligne circulaire.
Formule pour la circonférence
La circonférence d'un cercle C est calculée en multipliant le diamètre d par le nombre Pi (π = 3,1415...).
C = d × π
Définition de l'aire d'un cercle
L'aire d'un cercle A est l'aire délimitée par la ligne circulaire.
Formule pour l'aire d'un cercle
L'aire du cercle A est calculée en multipliant le carré du rayon r par Pi (π = 3,1415...).
A = r² × π
Comment calculez-vous le rayon à partir du diamètre ?
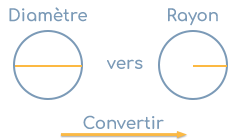
Soit un cercle de diamètre d de 20 cm. Nous recherchons le rayon r.
Calcul
Le rayon r est égal à la moitié du diamètre d, donc r = d / 2.
En substituant les 20 cm choisis dans l'exemple au diamètre d, le rayon du cercle est r = 20 cm / 2 = 10 cm.
Comment calculez-vous le rayon à partir de la circonférence ?
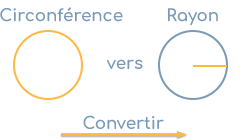
Soit un cercle de circonférence C de 30 cm. Nous recherchons le rayon r.
Calcul
La formule pour la circonférence est C = 2 × r × π. Lorsque nous convertissons cette formule en r, nous obtenons r = C / π / 2, qui est la moitié de la circonférence divisée par Pi (π = 3,1415...), ainsi r = C / π / 2.
Si l'on substitue les 30 cm choisis dans l'exemple à la circonférence C, le rayon du cercle est r = 30 cm / π / 2 = 4,77 cm.
Comment calculez-vous le rayon à partir de l'aire du cercle ?
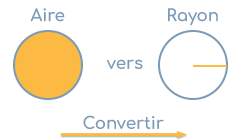
Soit une aire circulaire A de 100 cm². Nous recherchons le rayon r.
Calcul
La formule générale de l'aire circulaire A est A = r² × π. Si nous convertissons cette formule en r, le rayon r est égal à la racine carrée du résultat de l'aire circulaire A divisée par Pi (π = 3,1415...), ainsi r = A / π.
Si nous insérons les 100 cm² choisis dans l'exemple pour l'aire A, le rayon du cercle est r = 100 cm / π = 5,64 cm.
Comment calculez-vous le diamètre à partir du rayon?
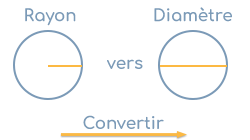
Soit un cercle de rayon r de 10 cm. Nous recherchons le diamètre d.
Calcul
Le diamètre d correspond au double du rayon r, c'est-à-dire d = 2 × r.
ISi les 10 cm choisis dans l'exemple sont utilisés pour le rayon r, le diamètre du cercle est d = 2 × 10 cm = 20 cm.
Comment calculez-vous le diamètre à partir de la circonférence ?
Soit un cercle de circonférence C de 30 cm. Nous recherchons le diamètre d.
Calcul
La formule pour la circonférence est C = d × π. Si nous convertissons cette formule en d, le diamètre d est égal à la circonférence divisée par Pi (π = 3,1415...), ainsi d = C / π.
Si l'on substitue les 30 cm choisis dans l'exemple à la circonférence C, le diamètre du cercle est d = 30 cm / π= 9,55 cm.
Comment calculez-vous le diamètre à partir de l'aire du cercle ?
Soit un cercle avec l'aire A de 100 cm². Nous recherchons le diamètre d.
Calcul
La formule générale pour l'aire du cercle A est A = r² × π. Comme le diamètre d correspond au double du rayon r, la formule est donc A = (d / 2)² × π. Si nous convertissons cette formule en d, le diamètre d est égal à deux fois la racine carrée de l'aire du cercle A divisée par Pi (π = 3,1415...), ainsi d = 2 × A / π.
Si l'on insère les 100 cm² choisis dans l'exemple pour l'aire A, le diamètre du cercle est d = 2 × 100 cm / π = 11,28 cm.
Comment calculez-vous la circonférence d'un cercle à partir du rayon ?
Soit un cercle de rayon r de 10 cm. Nous recherchons la circonférence U.
Calcul
TLa circonférence C correspond au double du rayon r multiplié par le nombre Pi (π = 3,1415...), ainsi C = 2 × r × π.
Si l'on insère les 10 cm choisis dans l'exemple pour le rayon r, la circonférence du cercle est C = 2 × 10 cm × π = 62,83 cm.
Comment calculez-vous la circonférence à partir du diamètre ?
Soit un cercle de diamètre d de 20 cm. Nous recherchons la circonférence U.
Calcul
La circonférence C correspond au diamètre d multiplié par le nombre Pi (π = 3,1415...), ainsi C = d × π.
Si l'on substitue les 20 cm choisis dans l'exemple au diamètre d, la circonférence du cercle est C = 20 cm × π = 62,83 cm.
Comment calculez-vous la circonférence d'un cercle à partir de son aire ?
Soit une aire circulaire A de 100 cm². Nous recherchons la circonférence U.
Calcul
La formule générale de l'aire circulaire A est A = r² × π. En utilisant cette formule, le rayon r peut maintenant être calculé en convertissant d'abord la formule en r. Le rayon r est égal à la racine carrée de l'aire circulaire A divisée par Pi (π = 3,1415...), ainsi r = A / π.
Si l'on insère les 100 cm² choisis dans l'exemple pour l'aire A, le rayon du cercle est r = 100 cm / π = 5,64 cm.
En utilisant le rayon ainsi calculé, on peut maintenant utiliser la formule générale de calcul de la circonférence : la circonférence C est égale au double du rayon r multiplié par le nombre Pi (π = 3,1415...), ainsi C = 2 × r × π.
Si l'on insère la valeur précédemment calculée pour le rayon r, la circonférence du cercle est C = 2 × 5,64 cm × π = 35,45 cm.
Comment calculez-vous l'aire d'un cercle à partir du rayon ?
Soit un cercle de rayon r de 10 cm. Nous cherchons l'aire du cercle A.
Calcul
L'aire du cercle A est égale au carré du rayon, c'est-à-dire r² multiplié par le nombre Pi (π = 3,1415...), et donc A = r² × π.
Si les 10 cm choisis dans l'exemple sont utilisés pour le rayon r, l'aire du cercle est la suivante A = (10 cm)² × π = 314,16 cm².
Comment calculez-vous l'aire d'un cercle à partir du diamètre ?
Soit un cercle de diamètre d de 20 cm. Nous cherchons l'aire du cercle A.
Calcul
L'aire A est égale à la moitié du diamètre au carré, c'est-à-dire (d / 2)² multiplié par le nombre Pi (π = 3,1415...) et donc A = (d / 2)² × π.
Si l'on substitue les 20 cm choisis dans l'exemple au diamètre d, l'aire du cercle est A = (20 cm / 2)² × π = 314,16 cm².
Comment calculez-vous l'aire d'un cercle à partir de la circonférence ?
Soit un cercle de circonférence C de 30 cm. Nous cherchons l'aire du cercle A.
Calcul
L'aire A est dérivée de la circonférence, par exemple, en déterminant d'abord le rayon du cercle r à partir de la circonférence. Ensuite, vous pouvez utiliser la formule commune pour l'aire d'un cercle, à savoir A = r² × π.
Le calcul du rayon basé sur la circonférence est déjà dérivé dans l'exemple pour la conversion de la circonférence en rayon et est de 4,77 cm.
Or, si l'on insère la valeur du rayon r calculée ici sur la base de la circonférence des 30 cm choisis dans l'exemple, à savoir 4,77 cm, l'aire du cercle est A = (4,77 cm)² × π = 71,62 cm².
Plus de calculateurs en ligne
Calculer un triangle, Convertir des superficies, Calculer des fractions, Convertisseur d'unités de temps, Calculateur pourcentage, Calcul en ligne, Convertisseur de longueur
Informations sur les sources
Nous avons utilisé, en particulier, les informations des sources suivantes pour la catégorie "Cercle"
Dernière mise à jour
Cette page de la catégorie "Cercle" a été modifiée ou revue pour la dernière fois par Michael Mühl le 19.02.2023. Elle correspond à l'état actuel.
Changements dans la catégorie "Cercle"
- Publication de la Calculateur de cercle.
- Révision éditoriale de cette page