Calculer un triangle

Calculer un triangle - calcul de l'aire, des côtés, des angles, du périmètre et de la hauteur

Triangle ﹣ Calculateur

Tout sur le triangle et son calcul : définitions, formules et calculs de l'aire du triangle, des longueurs de côté, du périmètre, des angles et des hauteurs. Le calculateur de triangle calcule toutes ces propriétés en utilisant seulement quelques spécifications nécessaires. Toutes les valeurs du triangle calculé et du triangle ainsi construit sont affichées dans le résultat du calculateur de triangle. Chaque calcul est dérivé à l'aide de la formule appropriée dans les "textes d'aide" du calculateur de triangle.

Ad

Contenu sur le thème "Calculer un triangle"

Calculateur ↑Contenu ↑

Définition d'un triangle

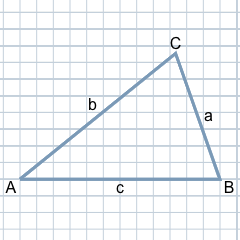Étiquette d'un triangle Un triangle peut être défini par trois points dans le plan qui ne se trouvent pas sur une ligne droite. Ces points sont appelés les coins du triangle. Les lignes de connexion entre deux coins sont les côtés du triangle. Le triangle délimite ainsi une surface dans le plan.

Les propriétés importantes d'un triangle sont son aire, la longueur de ses trois côtés, le périmètre du triangle, les angles des côtés les uns par rapport aux autres et les hauteurs de chaque côté par rapport au coin opposé. Le calcul de ces propriétés de triangle¬ et leur conversion à l'aide des formules correspondantes peuvent être effectuées de manière pratique avec le calculateur de triangle et seront discutées plus en détail ci-dessous.

Vous trouverez ici des articles séparés sur l'aire d'un triangle, le calcul des triangles rectangles et le calcul des triangles équilatéraux.
Calculateur ↑Contenu ↑

Étiquette d'un triangle

Comment s'appellent les trois coins d'un triangle ?

Dans un triangle, les trois coins sont généralement étiquetés avec les lettres majuscules A, B et C. L'étiquetage avec A, B et C se fait généralement dans le sens inverse des aiguilles d'une montre et commence par A dans le coin inférieur gauche.

Comment s'appellent les trois côtés d'un triangle ?

Les trois côtés d'un triangle sont étiquetés avec les lettres minuscules a, b et c. Le coin opposé latéral A est marqué a, le coin opposé latéral B est marqué b et le coin opposé latéral C est marqué c.

Comment s'appellent les trois angles d'un triangle ?

Les trois angles intérieurs d'un triangle sont désignés par les lettres grecques α (alpha), β (bêta) et γ (gamma). Ils sont situés aux coins correspondents, c'est-à-dire qu'au coin A, B et C, il y a un angle α, β et γ, respectivement.

Quelle est la hauteur d'un triangle ?

La hauteur d'un côté de base correspond à la distance perpendiculaire du point d'angle opposé au côté de base ou à son extension. Ainsi, la hauteur de a (ha) correspond à la distance entre le coin A et le côté opposé a auquel ha est perpendiculaire. En conséquence, les hauteurs de b (hb) et c (hc) sont définies.

Les autres lecteurs ont également lu

Aire d'un triangle
Triangle rectangle
Triangle équilatéral

Calculateur ↑Contenu ↑

Sélectionnez le bouton Aide à la saisie du calculateur de triangle pour calculer l'aire, les côtés, le périmètre, les angles et les hauteurs

Le calculateur pour calculer un triangle permet une sélection sous "Quelles valeurs sont données ?" au moyen de laquelle vous pouvez calculer un triangle en utilisant certaines valeurs données. Par conséquent, sélectionnez les valeurs connues disponibles pour le calcul du triangle. À l'aide de cette sélection, vous pouvez saisir les paramètres du triangle à calculer dans les champs qui s'affichent ensuite.

Le calculateur de triangle utilise les propriétés du triangle données pour calculer toutes les autres propriétés pertinentes pour le triangle et affiche également une représentation graphique, c'est-à-dire l'image du triangle..

Quelles valeurs sont données ?

Calculer un triangle : Valeurs données Veuillez sélectionner les valeurs du triangle disponibles pour calculer l'aire ou d'autres propriétés du triangle. Bien que l'aire d'un triangle puisse être calculée assez facilement en utilisant la première sélection "Un côté et la hauteur correspondante h", les deux saisies ne sont pas suffisantes pour calculer exactement un triangle entier à partir d'elles.

Afin de calculer un triangle de manière unique, d'autres valeurs données sont nécessaires : si les valeurs de l'une des autres options pouvant être sélectionnées ici sont données dans chaque cas, un triangle unique peut être construit pour celui-ci. Avec ces options, les abréviations correspondantes habituelles sont également affichées. Ici, "S" représente la correspondance d'une longueur de côté et "A" la correspondance d'un angle. Un triangle ne peut être calculé sans ambiguïté qu'en utilisant ces options. Par exemple, un triangle ne peut pas être déterminé sans ambiguïté sur la base de seulement trois angles donnés (AAA).

Dans ce qui suit, toutes les options sélectionnables, c'est-à-dire les combinaisons de valeurs données, sont décrites en détail.

Un côté et la hauteur correspondante h

Triangle: Un côté et la hauteur correspondante h

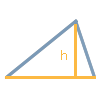
Veuillez sélectionner cette option si vous connaissez la longueur d'un côté a, b ou c du triangle et la hauteur correspondante. La hauteur d'un triangle au niveau d'un côté de base g correspond toujours à la distance perpendiculaire du point d'angle opposé au côté g ou à son extension. En utilisant la longueur d'un côté du triangle et la hauteur correspondante h, l'aire F du triangle peut être calculée. Cependant, le calcul des autres côtés et hauteurs ainsi que des angles n'est pas possible en utilisant ces deux valeurs données.

Les trois côtés a, b et c (CCC)

Triangle: Les trois côtés a, b et c (CCC)

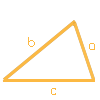
Veuillez sélectionner cette option si vous connaissez les longueurs des trois côtés du triangle. Lors du calcul des triangles, une constellation avec trois côtés donnés est souvent également abrégée en "SSS". En utilisant ces informations, le triangle entier peut être construit. Ainsi, l'aire et le périmètre du triangle, ainsi que les hauteurs de a, b et c, et les angles α, β et γ, peuvent être calculés.

Un côté d'un triangle équilatéral (CCC)

Equilateral triangle: Un côté d'un triangle équilatéral (CCC)

Veuillez sélectionner cette option si le triangle est équilatéral, c'est-à-dire qu'il a trois côtés de longueur égale avec une longueur connue a. Ce cas pour le triangle équilatéral est un cas particulier pour le calcul SSS dans le triangle général, puisque les trois côtés sont connus pour un côté donné. On pourrait également choisir l'option précédente "Les trois côtés a, b et c (CCC)" pour calculer le triangle, mais les formules simplifiées permettent le calcul du triangle équilatéral.

Pour calculer l'aire et toutes les autres propriétés du triangle, seule la longueur d'un côté est requise, puisque la longueur des trois côtés est donnée en même temps. Avec cela, toutes les autres propriétés du triangle peuvent être calculées et ainsi le triangle entier peut être construit.

Deux côtés avec un angle inclus (CAC)

Triangle: Deux côtés avec un angle inclus (CAC)

Veuillez sélectionner cette option si deux côtés du triangle sont connus avec l'angle qui les entoure. Lors du calcul des triangles, une constellation dans laquelle un angle et ses côtés englobants sont connus est souvent abrégée en "CACS". Cela peut être utilisé, par exemple, pour calculer la longueur du troisième côté, de sorte que toutes les autres propriétés du triangle puissent ensuite être calculées.

Deux côtés de cathète d'un triangle rectangle (CAC)

Triangle rectangle: Deux côtés de cathète d'un triangle rectangle (CAC)

Veuillez sélectionner cette option si vous connaissez les longueurs de ces deux côtés du triangle rectangle. Les cathètes sont les deux côtés qui se trouvent contre l'angle droit du triangle, tandis que le soi-disant hypoténuse se trouve en face de l'angle droit du triangle.

Ainsi, le cas avec deux cathètes données forme un cas particulier pour le calcul SAS dans le triangle général, puisque l'angle intermédiaire de 90 degrés est de toute façon connu. On pourrait donc également choisir l'option précédente "Deux côtés avec un angle inclus (CAC)" pour calculer le triangle, mais les formules simplifiées permettent le calcul du triangle rectangle.

S Ainsi, pour un triangle rectangle, ces deux côtés, à savoir les valeurs des deux cathètes, suffisent pour calculer toutes les autres propriétés du triangle et ainsi construire l'ensemble du triangle.

Un côté et deux angles (CAA, AAC ou ACA)

Triangle: Un côté et deux angles (CAA, AAC ou ACA)

Veuillez sélectionner cette option si un côté du triangle et deux angles quelconques sont connus. Lors du calcul des triangles, une constellation où un côté et deux angles sont connus est souvent abrégée en "AAS", " SAA " ou "ASA". Par exemple, le troisième angle peut être calculé en utilisant le théorème de la somme des angles, puis toutes les autres propriétés du triangle.

Deux côtés et un angle opposé au côté le plus long (SsA ou AsS)

Triangle: Deux côtés et un angle opposé au côté le plus long (CcA ou AcC)

Veuillez sélectionner cette option si deux côtés du triangle ainsi que l'angle opposé au côté le plus long donné sont connus. Lors du calcul des triangles, une constellation où deux côtés et l'angle opposé du côté le plus long sont connus est souvent également abrégée en "CcA" ou "AcC".

Ainsi, à l'aide du théorème du sinus, l'angle opposé au plus petit côté donné peut être calculé. Par la suite, le troisième angle peut être déterminé à l'aide du théorème de la somme des angles et enfin le triangle entier peut être calculé et construit de manière unique. Cependant, si seul l'angle opposé au côté donné le plus court est donné, le triangle ne peut pas être calculé sans ambiguïté.s

Calculateur ↑Contenu ↑

Exemples de calcul de triangle - CAC

Dans ce qui suit, nous vous montrons un exemple de calcul d'un triangle général où deux côtés et l'angle entre eux sont connus. Avec "C" comme abréviation de côté et "A" comme abréviation d'angle, cette constellation de propriétés données du triangle est également appelée "CAC".

Sur la base des trois valeurs données, les autres propriétés du triangle peuvent maintenant être déterminées sans ambiguïté étape par étape selon les théorèmes dits de congruence ("Quand un triangle est-il congruent avec un autre ?" ou "Quand un triangle est-il identique à un autre triangle à l'exception des déplacements ou des rotations ?").

Supposons qu'un triangle a un côté a = 4 cm et côté b = 6 cm, et l'angle γ fermé par les deux côtés a et b est de 70 degrés.

Explication

Nous recherchons le côté manquant c, le périmètre et l'aire du triangle, les deux angles restants α et β, et les hauteurs des trois côtés.

Vous pouvez entrer ces valeurs dans le calculateur de triangle après avoir sélectionné "Deux côtés avec un angle inclus (CAC)" sous "Quelles valeurs sont données ?". Le calculateur calculera ensuite, comme suit, toutes les valeurs que vous recherchez et affichera également un résultat graphique du triangle calculé.

Calculateur ↑Contenu ↑

Comment calcule-t-on le côté manquant d'un triangle ?

En utilisant les quantités données pour les côtés a et b ainsi que pour l'angle γ, la longueur du troisième côté inconnu c peut être calculée à l'aide du théorème général du cosinus pour c.

Formule : Théorème du cosinus pour c

c² = a² + b² − 2ab × cos γ°

et converti en c

c = a² + b² − 2ab × cos γ°

Insertion des valeurs existantes

En insérant les valeurs a = 4, b = 6 et γ = 70°, on obtient

c = 4² + 6² − 2 × 4 × 6 × cos 70° ≈ 5,97

Solution

Le troisième côté manquant c a une longueur de 5,97 cm.

Calculateur ↑Contenu ↑

Comment calcule-t-on le périmètre d'un triangle ?

En utilisant les longueurs données pour les côtés a et b et la longueur du côté c calculée entre-temps, le périmètre du triangle peut être déterminé comme suit :

Formule : périmètre P d'un triangle

Le périmètre du triangle est la somme des longueurs des trois côtés a, b et c.

P = a + b + c

Insertion des valeurs existantes

En insérant les valeurs données a = 4 et b = 6 et la valeur déjà calculée pour c = 5,97, on obtient

P = 4 + 6 + 5.97 = 15,97

Solution

La circonférence du triangle est de 15,97 cm.

Calculateur ↑Contenu ↑

Comment calcule-t-on l'aire d'un triangle

En utilisant les longueurs données pour les côtés a et b et la longueur du côté c calculée entre-temps, l'aire du triangle peut être calculée en utilisant la formule de Héron.

Formule : formule de Héron

A = s(s − a)(s − b)(s − c)

où s = la moitié de la circonférence, c'est-à-dire

s = (a + b + c) / 2

Insertion des valeurs existantes

En insérant les valeurs a = 4, b = 6 et c = 5,97, on obtient d'abord s avec

s = (4 + 6 + 5.97) / 2 = 7,98

Si nous insérons s = 7,98 dans la formule de Heron, nous obtenons finalement

A = 7.98(7.98 − 4)(7.98 − 6)(7.98 − 5.97)) ≈ 11.28

Solution

L'aire F du triangle est de 11,28 cm².

Calculateur ↑Contenu ↑

Comment sont calculés les angles manquants d'un triangle ?

Calcul de l'angle α

Nous calculons d'abord l'angle α. En utilisant les longueurs données pour les côtés a et b et la longueur du côté c calculée entre-temps, le Théorème général du cosinus pour le côté a peut être utilisé comme base de calcul de α.

Formule : Théorème du cosinus pour le côté a

a² = b² + c² − 2bc × cos α

Si l'on convertit le théorème du cosinus en α, on obtient

α = arccos( (b² + c² − a²) / 2bc )

Insertion des valeurs existantes

En insérant les valeurs a = 4, b = 6 et c = 5,97, on obtient

α = arccos((6² + 5,97² − 4²) / 2 × 6 × 5,97) = 0,68171 rad

La valeur qui vient d'être calculée est le radian de l'angle α, abrégé en "rad". Le radian est converti en degrés en utilisant la formule ci-dessous :

Formule : conversion du radian en degré

α° = α rad × 180 / π

En substituant le résultat intermédiaire α rad, on obtient

α° = 0,68171 rad × 180 / 3,14 ≈ 39,06°

Solution

'angle α du triangle est de 39,06°.

Calcul de l'angle β

Maintenant que l'angle α est calculé et que l'angle γ est de toute façon donné, l'angle restant β peut être calculé. Pour cela, le théorème de la somme des angles peut être utilisé.

Formule : Théorème de la somme des angles

La somme des trois angles intérieurs α, β et γ dans un triangle est toujours de 180 degrés.

α° + β° + γ° = 180°

Si l'on convertit le théorème de la somme des angles en β, on obtient

β° = 180° − α° − γ°

Insertion des valeurs existantes

En insérant l'angle déjà calculé pour α ainsi que l'angle donné γ, on obtient

β° = 180° − 39,06° − 70° = 70,94°

Solution

L'angle β du triangle est de 70,94°.

Calculateur ↑Contenu ↑

Comment sont calculées les hauteurs d'un triangle ?

Hauteur de a

Puisque tous les côtés et angles sont maintenant connus, la formule suivante peut être utilisée pour calculer la hauteur de a.

Formule pour la hauteur de a

ha = c × sin β

Insertion des valeurs existantes

Si on insère les valeurs pour le côté c déjà donné et l'angle β, on obtient

ha = 5,97 × sin 70,94° ≈ 5,64

Solution

La hauteur de a, c'est-à-dire ha est de 5,64.

Hauteur de b et hauteur de c

Les deux hauteurs peuvent être déterminées de manière analogue sur la base du calcul de la hauteur de a. Pour hb, hb = a × sin γ. Pour la hauteur en c, la formule hc = a × sin β s'applique. Après avoir inséré les valeurs concrètes, le calculateur de triangle calcule les résultats suivants pour les hauteurs restantes.

Solution

La hauteur de b, c'est-à-dire hb est de 3,76.

La hauteur de c, c'est-à-dire hc est de 3,78.

Calculateur ↑Contenu ↑

À quoi ressemble le triangle calculé ?

Le triangle calculé de cette manière, avec les côtés donnés a = 4 cm et b = 6 cm et un angle γ = 70 degrés, les deux côtés a et b peuvent être dessinés en utilisant toutes les valeurs calculées comme suit :

Result

Triangle calculé à partir de l'exemple donné

1 case équivaut à 0,5 unité (comme dans le livre d'arithmétique)

Plus de calculateurs en ligne

Calcul de cercle, Convertir des unités de superficie, Calculateur de fractions, Convertir les unités de temps, Calculateur de pourcentage, Calculateur, Convertir des unités de longueur, Convertir les chiffres romains

Informations sur les sources

Nous avons utilisé, en particulier, les informations des sources suivantes pour la catégorie "Triangle"

Dernière mise à jour le 20.02.2023

La page de la catégorie "Triangle" a été modifié pour la dernière fois par Michael Mühl le 20.02.2023. Par ailleurs, cette page est revue en permanence par les services d'édition et correspond à l'état actuel.

Changements dans la catégorie "Triangle"