Everything about the triangle and its calculation: definitions, formulas and calculations of the triangle's area, side lengths, perimeter, angles and heights. The triangle calculator calculates all these properties using just a few necessary specifications. All values of the calculated triangle and the triangle constructed in this way are displayed in the result of the triangle calculator. Each calculation is derived using the appropriate formula in the triangle calculator's 'help texts'.
Contents on the topic "Calculate Triangle"
Contents
Definition of Triangle
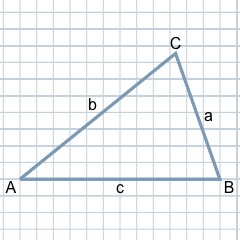 A triangle can be defined by three points in the plane that do not lie on a straight line. These points are called the corners of the triangle. The connecting lines between two corners are the sides of the triangle. The triangle thus delimits a surface in the plane.
A triangle can be defined by three points in the plane that do not lie on a straight line. These points are called the corners of the triangle. The connecting lines between two corners are the sides of the triangle. The triangle thus delimits a surface in the plane.
Important properties of a triangle are its area, the length of its three sides, the perimeter of the triangle, the angles of the sides to each other and the heights of each side to the opposite corner. The calculation of these triangleproperties and their conversion using corresponding formulae can be carried out conveniently with the triangle calculator and will be discussed in more detail below.
Label of the Triangle
What are the three corners of a triangle called?
In a triangle, the three corners are usually labelled with the capital letters A, B and C. The labelling with A, B and C is usually done counterclockwise and starts with A at the bottom-left corner.
What are the three sides of a triangle called?
The three sides of a triangle are labelled with the lower-case letters a, b and c. The side opposite corner A is labelled a, the side opposite corner B is labelled b and the side opposite corner C is labelled c.
What are the three angles of a triangle called?
The three inner angles of a triangle are designated by the Greek letters α (alpha), β (beta) and γ (gamma). They are located at the corresponding corners, i.e., at corner A, B and C there is an angle α, β and γ, respectively.
What is the height of a triangle?
The height of a base side corresponds to the perpendicular distance from the opposite corner point to the base side or its extension. Thus the height of a (ha) corresponds to the distance between the corner A and the opposite side a to which ha is perpendicular. Accordingly, the heights of b (hb) and c (hc) are defined.
What other readers have also read
Input 'Help' on the Triangle Calculator to calculate area, sides, perimeter, angles and heights
The calculator for calculating a triangle allows a selection under 'Which values are given?' by means of which you can calculate a triangle using certain given values. Therefore, select which known values are available for calculating the triangle. Using this selection, you can enter the parameters for the triangle to be calculated in the fields then displayed.
The triangle calculator uses the given triangle properties to calculate all other properties relevant to the triangle and also displays a graphic representation, i.e., the image of the triangle.
Which values are given?
 Please select which values of the triangle are available for calculating the area or other properties of the triangle. Although the area of a triangle can be calculated quite easily using the first selection "One side and corresponding height h", the two entries are not sufficient to calculate an entire triangle exactly from them.
Please select which values of the triangle are available for calculating the area or other properties of the triangle. Although the area of a triangle can be calculated quite easily using the first selection "One side and corresponding height h", the two entries are not sufficient to calculate an entire triangle exactly from them.
In order to calculate a triangle uniquely, other or further given values are required: If the values of one of the other options that can be selected here are given in each case, a unique triangle can be constructed for it. With these options, the usual matching abbreviations are also displayed. Here, "S" stands for the correspondence of a side length and "A" for the correspondence of an angle. A triangle can only be calculated unambiguously using these options. For example, a triangle cannot be unambiguously determined on the basis of only three given angles (AAA).
In the following, all selectable options, i.e., combinations of given values, are described in detail.
One side and corresponding height h
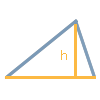
Please select this option if you know the length of a side a, b, or c of the triangle and the corresponding height. The height of a triangle at a base side g always corresponds to the perpendicular distance from the opposite corner point to the side g or its extension. Using the length of a side of the triangle and the corresponding height h, the area F of the triangle can be calculated. However, the calculation of the other sides and heights as well as the angles is not possible using these two given values.
All three sides a, b and c (SSS)
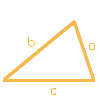
Please select this option if you know the lengths of all three sides of the triangle. When calculating triangles, a constellation with three given sides is often also abbreviated as 'SSS'. Using this information, the entire triangle can be constructed. Thus, the area and perimeter of the triangle, as well as the heights of a, b, and c, and the angles α, β and γ, can be calculated.
One side of an equilateral triangle (SSS)

Please select this option if the triangle is equilateral, i.e., it has three sides of equal length with known length a. This case for the equilateral triangle is a special case for the SSS calculation in the general triangle, since all three sides are known für a given side. One could also choose the previous option 'All three sides a, b and c (SSS)' to calculate the triangle, but the simplified formulas allow the calculation of the equilateral triangle.
To calculate the area and all other properties of the triangle, only the length of one side is required, since the length of all three sides is given at the same time. With this, all the other properties of the triangle can be calculated and thus the entire triangle can be constructed.
Two sides with an included angle (SAS)

Please select this option if two sides of the triangle are known together with the angle enclosed by them. When calculating triangles, a constellation in which an angle and its enclosing sides are known is often abbreviated as "SAS". This can be used, for example, to calculate the length of the third side, so that all other properties of the triangle can subsequently be calculated.
Two cathetus sides of a right triangle (SAS)

Please select this option if you know the lengths of these two sides of the right triangle. The cathetus are the two sides that lie against the right angle of the triangle, while the so-called hypotenuse lies opposite the right angle of the triangle.
Thus the case with two given cathethi forms a special case for the SAS calculation in the general triangle, since the intervening angle of 90 degrees is known anyway. One could therefore also choose the previous option "Two sides with an included angle (SAS)" to calculate the triangle, but the simplified formulas enable the calculation of the right triangle.
S So, for a right triangle, these two sides, namely the values of the two catheti, are sufficient to calculate all the other properties of the triangle and thus construct the entire triangle.
One side and two angles (SAA, AAS or ASA)

Please select this option if any side of the triangle and any two angles are known. When calculating triangles, a constellation where one side and two angles are known is often abbreviated as 'AAS', 'SAA' or 'ASA'. For example, the third angle can be calculated using the angle sum theorem and then all other properties of the triangle.
Two sides and an angle opposite the longer side (SsA or AsS)

Please select this option if two sides of the triangle as well as the angle opposite to the longer given side are known. When calculating triangles, a constellation where two sides and the opposite angle of the longer side are known is often also abbreviated as 'SsA' or 'AsS'.
Thus, with the help of the sine theorem, the angle opposite the smaller given side can be calculated. Subsequently, the third angle can be determined using the angle sum theorem and finally the entire triangle can be uniquely calculated and constructed. However, if only the angle opposite the shorter given side is given, the triangle cannot be calculated unambiguously.
Triangle Calculation Examples - SAS
In the following we show you an example of calculating a general triangle where two sides and the angle between them are known. With 'S' as the abbreviation for side and 'A' as the abbreviation for angle, this constellation of given properties of the triangle is also called 'SAS'.
On the basis of the three given values, the other properties of the triangle can now be determined unambiguously step by step according to the so-called congruence theorems ('When is a triangle congruent with another?' or 'When is a triangle identical with another triangle except for displacements or rotations?').
Assume a triangle has side a = 4 in and side b = 6 in, and the angle γ enclosed by the two sides a and b is 70 degrees.
Explanation
We are looking for the missing side c, the perimeter and the area of the triangle, the remaining two angles α and β, and the heights of all three sides.
You can enter these values into the triangle calculator after selecting 'Two sides with an included angle (SAS)' under 'What values are given?'. The calculator will then calculate, as follows, all the values you are looking for and will also output a graphical result of the calculated triangle.
How is the missing side of a triangle calculated?
Using the given quantities for the sides a and b as well as for the angle γ the length of the unknown third side c can be calculated with the help of the general cosine theorem for c.
Formula: Cosine theorem for c
c² = a² + b² − 2ab × cos γ°
and converted to c
c = a² + b² − 2ab × cos γ°
Inserting the existing values
Inserting the values a = 4, b = 6 and γ = 70°, we obtain
c = 4² + 6² − 2 × 4 × 6 × cos 70° ≈ 5.97
Solution
The missing third side c has a length of 5.97 in.
How is the perimeter of a triangle calculated?
Using the given lengths for sides a and b and the length of side c calculated in the meantime, the perimeter of the triangle can be determined as follows:
Formula: Perimeter U of a triangle
The perimeter of the triangle is the sum of the lengths of all three sides a, b and c.
U = a + b + c
Inserting the existing values
Inserting the given values a = 4 and b = 6 and the already calculated value for c = 5.97, we get
U = 4 + 6 + 5.97 = 15.97
Solution
The circumference of the triangle is 15.97 in.
How is the area of a triangle calculated?
Using the given lengths for sides a and b and the length of side c calculated in the meantime, the area of the triangle can be calculated using 'Heron's formula'.
Formula: Heron's formula
A = s(s − a)(s − b)(s − c)
where s = half the circumference, i.e.
s = (a + b + c) / 2
Inserting the existing values
Inserting the values a = 4, b = 6 and c = 5.97, we first obtain s with
s = (4 + 6 + 5.97) / 2 = 7.98
If we insert s = 7.98 into Heron's formula, we finally obtain
A = 7.98(7.98 − 4)(7.98 − 6)(7.98 − 5.97)) ≈ 11.28
Solution
The area A of the triangle is 11.28 in².
How are the missing angles of a triangle calculated?
Calculation of angle α
First we calculate the angle α. Using the given lengths for sides a and b and the length of side c calculated in the meantime, the general cosine theorem for side a can be used as the basis for calculating α.
Formula: Cosine theorem for side a
a² = b² + c² − 2bc × cos α
If one converts the cosine theorem to α, one obtains
α = arccos( (b² + c² − a²) / 2bc )
Inserting the existing values
Inserting the values a = 4, b = 6 and c = 5.97, we get
α = arccos((6² + 5.97² − 4²) / 2 × 6 × 5.97) = 0.68171 rad
The value just calculated is the radian of the angle α, abbreviated as 'rad'. The radian is converted to degrees using the formula below:
Formula: Conversion from radian to degree
α° = α rad × 180 / π
By substituting the intermediate result α rad, we obtain
α° = 0.68171 rad × 180 / 3.14 ≈ 39.06°
Solution
The angle α of the triangle is 39.06°.
Calculation of angle β
Now that the angle α is calculated and the angle γ is given anyway, the remaining angle β can be calculated. For this, the angle sum theorem can be used.
Formula: Angle sum theorem
The sum of the three interior angles α, β and γ in a triangle is always 180 degrees.
α° + β° + γ° = 180°
If one converts the angle sum theorem to β, one obtains
β° = 180° − α° − γ°
Inserting the existing values
Inserting the already calculated angle for α as well as the given angle γ, one obtains
β° = 180° − 39.06° − 70° = 70.94°
Solution
The angle β of the triangle is 70.94°.
How are the heights of a triangle calculated?
Height of a
Since all sides and angles are now known, the following formula can be used to calculate the height of a.
Formula for height of a
ha = c × sin β
Inserting the existing values
If we insert the values for the already given side c and the angle β, we obtain
ha = 5.97 × sin 70.94° ≈ 5.64
Solution
The height of a, i.e., ha is 5.64.
Height of b and height of c
Both heights can be determined analogously based on the calculation of the height of a. For hb, hb = a × sin γ. For the height at c, the formula hc = a × sin β applies. After inserting the concrete values, the triangle calculator calculates the following results for the remaining heights.
Solution
The height of b, i.e., hb is 3.76.
The height of c, i.e., hc is 3.78.
What does the calculated triangle look like?
The triangle calculated in this manner, with given sides a = 4 in and b = 6 in and an angle γ = 70 degrees enclosed by both sides a and b can be drawn using all of the calculated values as follows:
Result

1 box equals to 0.5 units (as in the arithmetic book)
More online calculators
Circle Calculation, Cylinder Calculation, Convert area units, Calculation Random Numbers, Fraction Calculator, Time Unit Converter, Percent Calculator, Calculator, Convert Length Units, Convert Roman Numerals
Source information
As source for the information in the 'Triangle' category, we have used in particular:
Last update
This page of the 'Triangle' category was last edited or reviewed by Michael Mühl on November 30, 2024. It corresponds to the current status.
Changes in this category "Triangle"
- Publication of an article Calculation of equilateral triangles.
- Publication of an article about Area of a triangle and about Right-angled triangles.
- Publication of the topic Calculate Triangle together with the corresponding texts.
- Editorial revision of this page

