Todo sobre los triángulos y sus cálculos: definiciones, fórmulas y cálculo del área, longitud de los lados, perímetro, ángulos y altura. La calculadora de triángulos permite determinar todas estas propiedades con unas pocas especificaciones. Todos los valores se muestran en los resultados de la calculadora de triángulos. Cada cálculo se obtiene utilizando la fórmula correspondiente que se muestra en los "textos de ayuda" de la calculadora.
Contenidos sobre el tema "Cálculo de triángulos"
Índice
Definición de triángulo
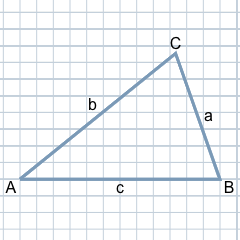 Un triángulo puede ser definido como tres puntos en el plano que no se encuentren en una misma línea recta. Estos puntos se llaman vértices. Las líneas que unen los vértices son los lados. El triángulo delimita así una superficie en el plano.
Un triángulo puede ser definido como tres puntos en el plano que no se encuentren en una misma línea recta. Estos puntos se llaman vértices. Las líneas que unen los vértices son los lados. El triángulo delimita así una superficie en el plano.
Las propiedades más importantes de un triángulo son el área, la longitud de sus lados, el perímetro, la relación entre los ángulos y las alturas de los lados (distancia entre un vértice y su lado opuesto). Con la calculadora de triángulos se pueden calcular fácilmente estas propiedades y hacer conversiones utilizando las fórmulas correspondientes, lo cual se tratará con más detalle a continuación.
Nomenclatura en los triángulos
¿Cómo se llaman los tres vértices de un triángulo?
En el triángulo, los tres vértices se suelen identificar con las letras mayúsculas A, B y C; normalmente, se comienza con la A en el vértice inferior izquierdo y se sigue en el sentido contrario al de las agujas del reloj.
¿Cómo se llaman los tres lados de un triángulo?
Los tres lados del triángulo se identifican con las letras minúsculas a, b y c. El lado opuesto al vértice A se llama a, el lado opuesto al vértice B se llama b y el lado opuesto al vértice C se llama c.
¿Cómo se llaman los tres ángulos del triángulo?
Los tres ángulos interiores de un triángulo se designan con las letras griegas α (alfa), β (beta) y γ (gamma). Están situados en los vértices correspondientes, es decir: en el vértice A, B y C hay sendos ángulos α, β y γ, respectivamente.
¿Cuál es la altura de un triángulo?
La altura es el segmento que une perpendicularmente un vértice con su lado opuesto o su prolongación. Por ejemplo, la altura ha corresponde a la distancia entre el vértice A y el lado opuesto al que es perpendicular, es decir, el lado a. Del mismo modo se definen las alturas de b (hb) y c (hc).
Otros usuarios han leído
Ayuda para introducir datos en la calculadora de triángulos para calcular el área, los lados, el perímetro, los ángulos y las alturas
La calculadora de triángulos permite seleccionar los valores requeridos para hacer cada cálculo específico. Por lo tanto, seleccione los valores con los que cuenta para realizar dichos cálculos. Puede introducir los parámetros del triángulo a calcular en los campos que se muestran a continuación.
La calculadora de triángulos utiliza las propiedades del triángulo introducidas para calcular todas las otras propiedades relevantes, y también ofrece una representación gráfica, es decir, la imagen del triángulo obtenido.
¿Qué valores se dan?
 Por favor, seleccione los valores del triángulo con los que cuenta para calcular el área u otras propiedades. Aunque el área de un triángulo se puede calcular con bastante facilidad utilizando la primera selección "uno de los lados y la altura correspondiente (h)", estos dos datos no son suficientes para calcular un triángulo completo.
Por favor, seleccione los valores del triángulo con los que cuenta para calcular el área u otras propiedades. Aunque el área de un triángulo se puede calcular con bastante facilidad utilizando la primera selección "uno de los lados y la altura correspondiente (h)", estos dos datos no son suficientes para calcular un triángulo completo.
Para calcular un triángulo con exactitud se necesitan otros valores: si se proporciona el valor de una de las otras opciones ya se podría construir un triángulo completo. Con estas opciones, también se muestran las abreviaturas habituales. Aquí "L" representa a los lados y "A" a los ángulos. Un triángulo solo se puede calcular de forma inequívoca con estas variables. Por ejemplo, un triángulo no puede determinarse de forma inequívoca con solo tres ángulos (AAA).
A continuación se describen detalladamente todas las opciones seleccionables, es decir, las combinaciones de los valores necesarios.
Un lado y su correspondiente altura (h)
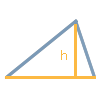
Seleccione esta opción si conoce la longitud de un lado del triángulo (a, b o c) y la altura correspondiente. La altura del lado es la distancia perpendicular entre dicho lado o su prolongación y el vértice opuesto. Utilizando la longitud de un lado y la altura correspondiente (h), se puede calcular el área (A) del triángulo. Sin embargo, el cálculo de los demás lados y alturas, así como de los ángulos, no es posible utilizando solo estos dos valores
Los tres lados a, b y c (LLL)
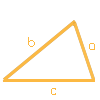
Por favor, seleccione esta opción si conoce las longitudes de los tres lados del triángulo. En el cálculo de triángulos, una congruencia de los tres lados se suele abreviar también como "LLL". Con esta información se puede construir el triángulo completo: se puede calcular el área y el perímetro, así como las alturas de a, b y c, y los ángulos α, β y γ.
Un lado de un triángulo equilátero (LLL)

Seleccione esta opción si el triángulo es equilátero, es decir, si tiene tres lados de igual longitud. Este es un caso especial para el cálculo LLL, ya que los tres lados son conocidos. También se podría elegir la opción anterior "los tres lados a, b y c (LLL)" para calcular el triángulo, pero los cálculos del triángulo equilátero se pueden hacer con las fórmulas simplificadas.
Para calcular el área y todas las demás propiedades de este triángulo solo se necesita la longitud de uno de los lados, ya que todas son iguales. Con esto se pueden calcular todas las demás propiedades y, por tanto, construir el triángulo completo.
Dos lados y el ángulo comprendido entre ellos (LAL)

Por favor, seleccione esta opción si conoce dos lados del triángulo junto con el ángulo que conforman. En el cálculo de triángulos, cuando se conoce un ángulo y los lados que lo componen, se suele abreviar como "LAL". Esto se puede utilizar, por ejemplo, para calcular la longitud del tercer lado y, a continuación, todas las demás propiedades del triángulo.
Dos catetos de un triángulo rectángulo (LAL)

Por favor, seleccione esta opción si conoce las longitudes de estos dos lados del triángulo rectángulo. Los catetos son los dos lados que se encuentran en el ángulo recto, mientras que la hipotenusa es el lado opuesto al ángulo recto.
Este es un caso especial para el cálculo LAL, ya que se conoce que hay un ángulo de 90 grados. También se podría elegir la opción anterior "dos lados y el ángulo comprendido entre ellos (LAL)", pero el triángulo rectángulo se puede calcular con las fórmulas simplificadas.
En el caso del triángulo rectángulo, estos dos lados (los valores de los catetos) son suficientes para calcular todas las demás propiedades y construir el triángulo completo.
Un lado y dos ángulos (LAA, AAL o ALA)

Por favor, seleccione esta opción si conoce algún lado del triángulo y dos ángulos cualesquiera. Al calcular triángulos, si se conoce un lado y dos ángulos se puede abreviar como "AAL", "LAA" o "ALA". Por ejemplo, el tercer ángulo se puede calcular utilizando el teorema de la suma de los ángulos y luego obtener todas las demás propiedades del triángulo.
Dos lados y el ángulo opuesto al lado más largo (LLA o ALL)

Por favor, seleccione esta opción si se conocen dos lados del triángulo y el ángulo opuesto al lado más largo. En el cálculo de triángulos, si se conocen dos lados y el ángulo opuesto del lado más largo se puede abreviar como "LlA" o "AlL".
Utilizando el teorema de los senos se puede calcular el ángulo opuesto al lado menor; luego se podrá determinar el tercer ángulo mediante el teorema de la suma de los ángulos y, finalmente, calcular y construir el triángulo completo. Sin embargo, si solo se proporciona el ángulo opuesto al lado menor, el triángulo no puede calcularse inequívocamente.
Ejemplos de cálculo de triángulos - LAL
A continuación se muestra un ejemplo de cálculo de un triángulo del que se conocen dos lados y el ángulo conformado entre ellos. Siendo L la abreviatura de "lado" y A la abreviatura de "ángulo", a este conjunto de propiedades se lo llama también "LAL".
A partir de estos tres valores, se pueden determinar las demás propiedades del triángulo de forma inequívoca con los teoremas de congruencia (¿cuándo un triángulo es congruente con otro?" o "¿cuándo un triángulo es idéntico a otro triángulo, salvo por los desplazamientos y las rotaciones?").
Tenemos un triángulo con lado a = 4 cm y lado b = 6 cm, cuyo ángulo γ comprendido entre a y b es de 70 grados.
Explicación
Buscamos el lado c, el perímetro, el área, los ángulos α y β y las alturas de los tres lados.
Se pueden introducir estos valores en la calculadora de triángulos después de seleccionar "Dos lados y el ángulo comprendido entre ellos (LAL)" en "¿Qué valores se dan?". Como se indica a continuación, la calculadora determinará entonces todos los valores requeridos y mostrará un gráfico del triángulo obtenido.
¿Cómo se calcula el lado faltante del triángulo?
Utilizando los valores de los lados a y b y del ángulo γ se puede calcular la longitud del tercer lado (c) con la ayuda del teorema del coseno.
Fórmula: Teorema del coseno para c
c² = a² + b² − 2ab × cos γ°
y convertido a c
c = a² + b² − 2ab × cos γ°
Inserción de los valores existentes
Insertando los valores a = 4, b = 6 y γ = 70°, obtenemos
c = 4² + 6² − 2 × 4 × 6 × cos 70° ≈ 5,97
Solución
El tercer lado faltante (c) tiene una longitud de 5.97 cm.
¿Cómo se calcula el perímetro de un triángulo?
Utilizando las longitudes conocidas de los lados a y b y la longitud calculada del lado c, se puede determinar el perímetro de la siguiente manera:
Fórmula: perímetro (P) de un triángulo
El perímetro del triángulo es la suma de las longitudes de los tres lados: a, b y c.
P = a + b + c
Inserción de los valores existentes
Insertando los valores conocidos de a = 4 y b = 6, y el valor ya calculado para c = 5,97, obtenemos
P = 4 + 6 + 5,97 = 15,97
Solución
El perímetro del triángulo es de 15.97 cm.
¿Cómo se calcula el área de un triángulo?
Con las longitudes conocidas de los lados a y b y la longitud calculada para c, se puede calcular el área del triángulo utilizando la fórmula de Herón.
Fórmula: fórmula de Herón
A = s(s − a)(s − b)(s − c)
donde s es igual a la mitad del perímetro (el semiperímetro), es decir:
s = (a + b + c) / 2
Inserción de los valores existentes
Insertando los valores a = 4, b = 6 y c = 5,97, obtenemos primero s
s = (4 + 6 + 5,97) / 2 = 7,98
Si insertamos el valor de s = 7,98 en la fórmula de Herón, finalmente obtenemos
A = 7,98(7,98 − 4)(7,98 − 6)(7,98 − 5,97)) ≈ 11,28
Solución
El área (A) del triángulo es de 11.28 cm².
¿Cómo se calculan los ángulos faltantes de un triángulo?
Cálculo del ángulo α
Primero calculamos el ángulo α. Utilizando las longitudes conocidas de los lados a y b y la longitud calculada para el lado c, se puede aplicar el teorema del coseno para el lado a y así calcular α.
Fórmula: teorema del coseno para el lado a
a² = b² + c² − 2bc × cos α
Si se convierte el teorema del coseno a α, se obtiene
α = arcos( (b² + c² − a²) / 2bc )
Inserción de los valores existentes
Insertando los valores a = 4, b = 6 y c = 5,97, obtenemos
α = arcos((6² + 5,97² − 4²) / 2 × 6 × 5,97) = 0,68171 rad
El valor que se acaba de calcular es el radián del ángulo α, abreviado como "rad". El radián se convierte en grados mediante la siguiente fórmula:
Fórmula: conversión de radián a grados
α° = α rad × 180 / π
Sustituyendo el resultado intermedio α rad, obtenemos
α° = 0,68171 rad × 180 / 3,14 ≈ 39,06°
Solución
El ángulo α del triángulo es de 39,06°.
Cálculo del ángulo β
Ahora que ya se ha calculado el ángulo α y se conoce el ángulo γ, se puede calcular el ángulo β. Para ello, se puede utilizar el teorema de la suma de los ángulos.
Fórmula: teorema de la suma de los ángulos
La suma de los tres ángulos interiores α, β y γ de un triángulo es siempre 180 grados.
α° + β° + γ° = 180°
Si se convierte el teorema de la suma de los ángulos a β, se obtiene
β° = 180° − α° − γ°
Inserción de los valores existentes
Insertando el ángulo ya calculado para α así como el ángulo dado γ, se obtiene
β° = 180° − 39,06° − 70° = 70,94°
Solución
El ángulo β del triángulo es de 70.94°.
¿Cómo se calculan las alturas de un triángulo?
Altura de a
Como ya se conocen todos los lados y ángulos del triángulo, se puede utilizar la siguiente fórmula para calcular la altura de a.
Fórmula para calcular la altura de a
ha = c × sen β
Inserción de los valores existentes
Si insertamos los valores del lado c y del ángulo β, obtenemos
ha = 5,97 × sen 70,94° ≈ 5,64
Solución
La altura de a, es decir, ha es 5,64.
Altura de b y de c
Ambas alturas pueden determinarse análogamente a partir del cálculo de la altura de a. Para la altura de b se aplica la fórmula
hb = a × sen γ; para la altura de c se aplica la fórmula hc = a × sen β. Después de insertar los valores, la calculadora de triángulos obtiene los resultados para las demás alturas.
Solución
La altura de b, es decir, hb es 3,76.
La altura de c, es decir, hc es 3,78.
¿Qué aspecto tiene el triángulo calculado?
El triángulo calculado de esta manera, con los lados a = 4 cm y b = 6 cm , y el ángulo γ = 70 grados conformado entre los lados a y b se puede graficar como sigue:
Resultado

1 casilla equivale a 0,5 unidades (como en el cuaderno de matemáticas).
Otras calculadoras online
Cálculo del círculo, Convertir unidades de superficie, Calcular fracciones, Convertir unidades de tiempo, Calculadora de porcentajes, Calculadora, Convertir unidades de longitud, Convertir a números romanos
Referencias
Como fuente de información en la categoría de "Triángulo", hemos utilizado en particular:
Última actualización
Esta página de la categoría "Triángulo" fue editada o revisada por última vez el 30.11.2024 por Michael Mühl. Corresponde al estado actual.
Cambios en esta categoría "Triángulo"
- Publicación del artículo Cálculo de triángulos equiláteros.
- Publicación del artículo sobre Área de un triángulo y Triángulos rectángulos.
- Publicación del tema Calcular triángulo junto con los textos correspondientes.
- Revisión editorial de esta página

