Compared to general triangles, an equilateral triangle is a special type of triangle because it has three sides of exactly the same length. In the following section, we will use an example with a given side length to calculate the area, the perimeter, the angles and the heights for the equilateral triangle. To do this, we will use the formulas and calculation rules that have been simplified specifically for equilateral triangles.
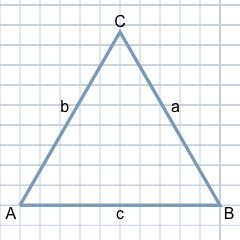Before we go into the calculation of equilateral triangles in more detail, here is a brief definition of the equilateral triangle.
Basically, a triangle is defined by three points in the plane that do not lie on a straight line. The three points form the corners of the triangle. Each connecting line between two such corners is a side of the triangle. In the plane, the triangle therefore delimits a surface.
The special feature of the equilateral triangle compared to the general triangle is that all three sides of the triangle have the same length, as the figure shown here illustrates.
By default, the clockwise corners are labelled with the uppercase letters A, B, C. The sides opposite these corners are given the corresponding lowercase letters a, b and c. In the case of an equilateral triangle, all three sides are usually labelled a.
Introduction to the Calculation of Equilateral Triangles
Equilateral triangles differ from general triangles only in that all three sides have the same length. Basically, a triangle can be unambiguously determined if all three sides a, b and c are known. Therefore, it is sufficient to calculate an equilateral triangle if only one side is known.
However, in the case of the equilateral triangle with a given side a, simpler calculations are also possible. For example, all three angles in the equilateral triangle are also always equal and always amount to 60 degrees. Likewise, the calculation of the area of an equilateral triangle follows a simpler formula than, for example, in the case of the general triangle with three given sides a, b and c, as we will see below.
Example for the calculation of an equilateral triangle
Below we show an example of the calculation of an equilateral triangle where the side length a is known. Using this one given value, the other properties of the equilateral triangle can now be clearly determined step by step.
Example
Let the side length a = 5 in be given. Since it is an equilateral triangle, the value of all three sides is already known.
Explanation
We are looking for the area, the perimeter, the angles and the heights of all three sides of the equilateral triangle.
You can enter the given value for side a into the equilateral triangle calculator after selecting "One side for an equilateral triangle" under "What values are given?". The calculator will then calculate, as in the following calculations, all the values sought for the triangle and will also output a graphical result of the calculated triangle.
How is the area in an equilateral triangle calculated?
In an equilateral triangle, as the name implies, all three sides are of equal length. Therefore, the following simplified formula applies to the area of the equilateral triangle, where a is the length of one of the sides
Formula for area of an equilateral triangle
A = 3 / 4 × a²
Inserting the existing value for the page length
If you insert the value for a, you get
A = 3 / 4 × 5² ≈ 10.83 in²
Solution
The area A of the equilateral triangle is 10.83 in².
How are the heights in the equilateral triangle calculated?
To calculate the height of a in the equilateral triangle, the following formula can be used instead of the more complicated formula for general triangles:
Formula for height of a in the equilateral triangle
ha = 3 / 2 × a
Inserting the existing values
Substituting the known value for a = 5 in, we obtain
ha = 3 / 2 × 5 ≈ 4.33
Solution
The height of a, i.e., ha is 4.33 in.
Since sides b and c are exactly as long as a, their heights are also identical to a.
Before we go into the calculation of equilateral triangles in more detail, here is a brief definition of the equilateral triangle.