Tudo sobre o triângulo e o seu cálculo: definições, fórmulas e cálculos da área, comprimentos dos lados, perímetro, ângulos e alturas do triângulo. A calculadora de triângulos calcula todas estas propriedades utilizando apenas algumas informações necessárias. Todos os valores do triângulo calculado e do triângulo construído desta forma são exibidos no resultado da calculadora de triângulos. Cada cálculo é obtido utilizando a devida fórmula nos “textos de ajuda” da calculadora de triângulos.
Índice do tópico "Calcular um triângulo"
Conteúdos
Definição do triângulo
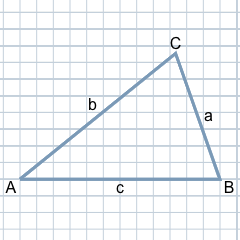 Um triângulo pode ser definido por três pontos no plano que não se encontram numa linha reta. Estes pontos designam-se por cantos do triângulo. As linhas que estabelecem a ligação entre dois cantos são os lados do triângulo. Assim sendo, o triângulo delimita uma superfície no plano.
Um triângulo pode ser definido por três pontos no plano que não se encontram numa linha reta. Estes pontos designam-se por cantos do triângulo. As linhas que estabelecem a ligação entre dois cantos são os lados do triângulo. Assim sendo, o triângulo delimita uma superfície no plano.
As propriedades importantes de um triângulo são a sua área, o comprimento dos seus três lados, o perímetro do triângulo, os ângulos dos lados em relação uns aos outros e as alturas de cada lado em relação ao canto oposto. O cálculo destas propriedades do triângulo e a sua conversão utilizando a fórmula correspondente podem ser convenientemente executados com a calculadora de triângulo e seráo discutidos mais detalhadamente abaixo.
Identificação do triângulo
Como se identificam os três cantos de um triângulo?
Num triângulo, os três cantos são habitualmente identificados com as letras maiúsculas A, B e C. A identificação com A, B e C é habitualmente realizada no sentido anti-horário e começa com A no canto inferior esquerdo.
Como se identificam os três lados de um triângulo?
Os três lados de um triângulo são identificados com as letras minúsculas a, b e c. O lado oposto ao canto A é identificado com a, o lado oposto ao canto B é identificado com b e o lado oposto ao canto C é identificado com c.
Como se identificam os três ângulos de um triângulo?
Os três ângulos de um triângulo são designados pelas letras gregas α (alfa), β (beta) e γ (gama). Eles estão localizados nos cantos correspondentes, isto é, no canto A, B e C encontra-se o ângulo α, β e γ, respetivamente.
Qual é a altura de um triângulo?
A altura de um lado da base corresponde à distância perpendicular do ponto do canto oposto ao lado da base ou a sua extensão. Assim sendo, a altura de a (ha) corresponde à distância entre o canto A e o lado oposto a para o qual ha é perpendicular. Consequentemente, as alturas de b (hb) e c (hc) são definidas.
O que os outros leitores também leram
"Ajuda" na calculadora dependente triângulo para calcular a área, os lados, o perímetro, os ângulos e as alturas
A calculadora para calcular um triângulo permite uma seleção em “Que valores são conhecidos?” através dos quais pode calcular um triângulo utilizando determinados valores conhecidos. Por conseguinte, selecione que valores conhecidos se encontram disponíveis para calcular o triângulo. Utilizando esta seleção, pode inserir os parâmetros para o triângulo ser calculado nos campos e, de seguida, exibidos.
A calculadora do triângulo utiliza as propriedades conhecidas do triângulo para calcular todas as outras propriedades relevantes do triângulo e também exibe uma representação gráfica, isto é, a imagem do triângulo.
Que valores são conhecidos?
 Selecione que valores do triângulo estão disponíveis para calcular a área ou outras propriedades do triângulo. Embora a área de um triângulo possa ser calculada muito facilmente utilizando a primeira seleção “Um lado e a altura h correspondente”, as duas entradas não são suficientes para calcular todo um triângulo exatamente a partir delas.
Selecione que valores do triângulo estão disponíveis para calcular a área ou outras propriedades do triângulo. Embora a área de um triângulo possa ser calculada muito facilmente utilizando a primeira seleção “Um lado e a altura h correspondente”, as duas entradas não são suficientes para calcular todo um triângulo exatamente a partir delas.
Para calcular um triângulo, outros ou determinados valores dados são necessários: se os valores de uma das outras opções que podem ser selecionadas aqui são conhecidos, em cada caso, pode ser construído um triângulo único. Com estas opções, as habituais abreviaturas correspondentes também são exibidas. Aqui, "S" significa a correspondência do comprimento de um lado e “A” para a correspondência de um ângulo. Um triângulo só pode ser calculado inequivocamente utilizando estas opções. Por exemplo, um triângulo não pode ser inequivocamente determinado tendo como base apenas três ângulos conhecidos (AAA).
No seguinte, todas as opções selecionáveis, isto é, combinações de valores conhecidos, são descritos em detalhe.
Um lado e a altura h correspondente
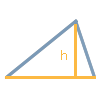
Selecione esta opção se souber o comprimento de um lado a, b ou c do triângulo e a altura correspondente. A altura de um triângulo num lado da base g corresponde sempre à distância perpendicular do ponto do canto oposto para o lado g ou a sua extensão. Utilizando o comprimento de um lado do triângulo e a altura h correspondente, a área A do triângulo pode ser calculada. No entanto, o cálculo dos outros lados e alturas, bem como dos ângulos não é possível utilizando estes dois valores conhecidos.
Todos os três lados a, b e c (LLL)
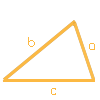
Selecione esta opção caso conheça os comprimentos de todos os três lados do triângulo. Quando calcula os triângulos, uma constelação com três lados conhecidos também é frequentemente abreviada como “LLL”. Utilizando estas informações, é possível construir qualquer triângulo. Assim sendo, a área e o perímetro do triângulo, bem como as alturas a, b e c e os ângulos α, β e γ, podem ser calculados.
Um lado de um triângulo equilátero (LLL)

Selecione esta opção caso o triângulo seja equilátero, ou seja, tenha três lados de igual comprimento com o comprimento a conhecido. Este caso para o triângulo equilátero é um caso especial para o cálculo SSS no triângulo geral, dado que todos os três lados são conhecidos para um lado conhecido. Também podemos escolher a opção anterior 'Todos os três lados a, b e c (LLL)' para calcular o triângulo, mas as fórmulas simplificadas permitem o cálculo do triângulo equilátero.
Para calcular a área e todas as outras propriedades do triângulo, apenas o comprimento de um lado é necessário, dado que o comprimento de todos os três lados é dado ao mesmo tempo. Assim sendo, todas as outras propriedades do triângulo podem ser calculadas e, por conseguinte, pode ser construído qualquer triângulo.
Dois lados com um ângulo incluído (LAL)

Selecione esta opção se forem conhecidos dois lados do triângulo com um ângulo entre eles. Quando calcula triângulos, uma constelação na qual um ângulo e os seus lados adjacentes são conhecidos é frequentemente abreviada como “SAS”. Isto pode ser utilizado, por exemplo, para calcular o comprimento do terceiro lado, de forma que todas as outras propriedades do triângulo podem subsequentemente ser calculadas.
Dois lados catetos de um triângulo retângulo (LAL)

Selecione esta opção caso conheça os comprimentos destes dois lados do triângulo retângulo. Os catetos são os dois lados que se encontram no ângulo retângulo do triângulo, enquanto a designada hipotenusa encontra-se do lado oposto do ângulo reto do triângulo.
Assim sendo, o caso com dois lados conhecidos forma um caso especial para o cálculo SAS no triângulo geral, dado que o ângulo que intervém de 90 graus já é conhecido. Por conseguinte, também poderá escolher a opção anterior 'Dois lados com um ângulo incluído (LAL)' para calcular o triângulo, mas as fórmulas simplificadas permitem o cálculo do triângulo retângulo.
S Assim sendo, para um triângulo retângulo, estes dois lados, nomeadamente os valores de dois catetos, são o suficiente para calcular todas as outras propriedades do triângulo e, assim, construir qualquer triângulo.
Um lado e dois ângulos (LAA, AAL ou ALA)

Selecione esta opção se um dos lados do triângulo e dois ângulos são conhecidos. Ao calcula triângulos, uma constelação onde um lado e dois ângulos são conhecidos é frequentemente abreviada como 'AAL', 'LAA' ou 'ALA'. Por exemplo, o terceiro ângulo pode ser calculado utilizando o teorema da soma do ângulo e, de seguida, todas as outras propriedades do triângulo.
Dois lados e um ângulo oposto ao lado mais comprido (LlA ou AlL)

Selecione esta opção se dois lados do triângulo bem como o ângulo oposto ao lado mais comprido são conhecidos. Ao calcular triângulos, uma constelação onde dois lados e o ângulo oposto ao lado mais comprido são conhecidos é frequentemente abreviads como 'LlA' ou 'AlL'.
Assim sendo, com a ajuda do teorema do seno, o ângulo oposto ao lado mais pequeno conhecido pode ser calculado. Subsequentemente, o terceiro ângulo pode ser determinado utilizando o teorema da soma dos ângulos e finalmente qualquer triângulo pode ser calculado e construído. No entanto, se apenas o ângulo oposto ao lado mais curto é conhecido, o triângulo não pode ser inequivocamente calculado.
Exemplos do cálculo do triângulo - LAL
De seguinte, mostramos-lhe um exemplo do cálculo de um triângulo geral onde dois lados e o ângulo entre estes são conhecidos. Com 'L' como a abreviatura para o lado e 'A' como a abreviatura para o ângulo, esta constelação das propriedades conhecidas do triângulo também é designada 'LAL'.
Tendo como base os três valores dados, as outras propriedades do triângulo podem ser determinadas inequivocamente passo a passo segundo os designados teoremas da congruência ('Quando é que um triângulo é congruente com outro?' ou 'Quando é que um triângulo idêntico a outro triângulo exceto para deslocamentos ou rotações?').
Assumamos que um triângulo tem lado a = 4 cm e o lado b = 6 cm, e o ângulo γ entre estes dois lados a e b é 70 graus.
Explicação
Estamos à procura do lado c em falta, o perímetro e a área do triângulo, os restantes dois ângulos α e β e as alturas de todos os três lados.
Pode inserir estes valores na calculadora do triângulo após selecionar 'Dois lados com um ângulo incluído (LAL)' em 'Que valores são conhecidos?'. A calculadora calculará então todos os valores que procura e exibirá um resultado gráfico do triângulo calculado.
Como é calculado o lado em falta de um triângulo?
Utilizando as quantidades dadas para os lados a e b, bem como para o ângulo γ, o comprimento do terceiro lado c desconhecido pode ser calculado com a ajuda do teorema geral do cosseno para c.
Fórmula: teorema do cosseno para c
c² = a² + b² − 2ab × cos γ°
e convertido para c
c = a² + b² − 2ab × cos γ°
Inserindo os valores existentes
Inserindo os valores a = 4, b = 6 e γ = 70°, obtemos
c = 4² + 6² − 2 × 4 × 6 × cos 70° ≈ 5,97
Solução
O terceiro lado c em falta tem um comprimento de 5,97 cm.
Como é calculado o perímetro de um triângulo?
Utilizando os comprimentos conhecido para os lados a e b e o comprimento do lado c calculado, o perímetro do triângulo pode ser determinado da seguinte forma:
Fórmula: perímetro P de um triângulo
O perímetro do triângulo é a soma dos comprimentos de todos os três lados a, b e c.
P = a + b + c
Inserindo os valores existentes
Inserindo os valores existentes a = 4 e b = 6 e o valor já calculado para c = 5,97, obtemos
P = 4 + 6 + 5,97 = 15,97
Solução
A circunferência do triângulo é 15,97 cm.
Como é calculada a área de um triângulo?
Utilizando os comprimentos conhecidos para os lados a e b e o comprimento do lado c calculado entretanto, a área do triângulo pode ser calculada utilizando a 'fórmula de Heron'.
Fórmula: fórmula de Heron
F = s(s − a)(s − b)(s − c)
onde s = metade da circunferência, isto é,
s = (a + b + c) / 2
Inserindo os valores existentes
Inserindo os valores a = 4, b = 6 e c = 5,97, obtemos primeiro s com
s = (4 + 6 + 5,97) / 2 = 7,98
Se inserirmos s = 7,98 na fórmula de Heron, obtemos finalmente
A = 7,98(7,98 − 4)(7,98 − 6)(7,98 − 5,97)) ≈ 11,28
Solução
A área A do triângulo é 11,28 cm².
Como são calculados os ângulos em falta de um triângulo?
Cálculo do ângulo α
Primeiro, calculamos o ângulo α. Utilizando os comprimentos conhecidos para os lados a e b e o comprimento do lado c calculado entretanto, o teorema geral do cosseno para o lado a utilizado como a base para o cálculo de α.
Fórmula: teorema do cosseno para o lado a
a² = b² + c² − 2bc × cos α
Se converter o teorema do cosseno para α, obtemos
α = arccos( (b² + c² − a²) / 2bc )
Inserindo os valores existentes
Inserindo os valores a = 4, b = 6 e c = 5,97, obtemos
α = arccos((6² + 5,97² − 4²) / 2 × 6 × 5,97) = 0,68171 rad
O valor que acabou de ser calculado é o radiano do ângulo α, abreviado como 'rad'. O radiano é convertido para graus utilizando a fórmula abaixo:
Fórmula: conversão de radiano para graus
α° = α rad × 180 / π
Substituindo o resultado intermédio α rad, obtemos
α° = 0,68171 rad × 180 / 3,14 ≈ 39,06°
Solução
O ângulo α do triângulo é 39,06°.
Cálculo do ângulo β
Agora que o ângulo α está calculado e o ângulo γ é conhecido, o restante ângulo β pode ser calculado. Para isso, o teorema da soma do ângulo pode ser usado.
Fórmula: teorema da soma dos ângulos
A soma dos três ângulos interiores α, β e γ num triângulo é sempre 180 graus.
α° + β° + γ° = 180°
Se convertermos o teorema da soma dos ângulos para β, obtemos
β° = 180° − α° − γ°
Inserindo os valores existentes
Inserindo o ângulo já calculado para α, bem como o ângulo conhecido γ, obtemos
β° = 180° − 39.06° − 70° = 70,94°
Solução
O ângulo β do triângulo é 70,94°.
Como são calculadas as alturas de um triângulo?
Altura de a
Dado que todos os lados e ângulos já são conhecidos, a seguinte fórmula pode ser utilizada para calcular a altura de a.
Fórmula para a altura de a
ha = c × sin β
Inserindo os valores existentes
Se inserirmos os valores para o lado c já conhecido e o ângulo β, obtemos
ha = 5,97 × sin 70,94° ≈ 5,64
Solução
A altura de a, ou a é 5,64.
Altura de b e altura de c
Ambas as alturas podem ser determinadas analogamente tendo como base o cálculo da altura de a. Para hb, hb = a × sin γ. Para a altura em c, a fórmula hc = a × sin β aplica-se. Após inserir os valores concretos, a calculadora de triângulo calcula os seguintes resultados para as alturas restantes.
Solução
A altura de b, ou hb is 3,76.
A altura de c, ou hc is 3,78.
Como é representado o triângulo calculado?
O triângulo calculado desta forma, com os lados dados a = 4 cm e b = 6 cm e um ângulo γ = 70 graus entre ambos os lados a e b pode ser desenhado utilizando todos os valores calculados da seguinte forma:
Resultado

1 quadrado equivale a 0,5 unidades (como no livro aritmético)
Mais calculadoras online
Cálculo do círculo, Converter Unidades de área, Cálculo de números aleatórios, Calculadora de frações, Converter unidades de tempo, Calculadora percentual, Calculadora, Converter unidades de comprimento, Converter numeração romana
Fonte de informação
Como fonte de informação na categoria "Triângulo", utilizámos nomeadamente:
Última atualização
Esta página da categoria "Triângulo" foi editada ou revista pela última vez por Michael Mühl em 30.11.2024. Corresponde ao estado atual.
Alterações desta categoria "Triângulo"
- Publicação do artigo Cálculo de triângulos equiláteros.
- Publicação do artigo Área de um triângulo e Triângulos de ângulo recto.
- Publicação do tópico Calcular um triângulo juntamente com os textos correspondentes.
- Revisão editorial desta página

