A right triangle is a special type of triangle compared to general triangles because, as the name suggests, it has a right angle or a 90-degree angle.
In the following section, we will use examples to calculate all the important values of the right triangle using the special formulas and calculation rules for right triangles.
On the page of our Triangle Calculator you will find a lot of information on calculating not only right triangles but also general triangles. Alternatively, visit our guides on the topics 'Area of a Triangle' and 'Equilateral Triangles'.
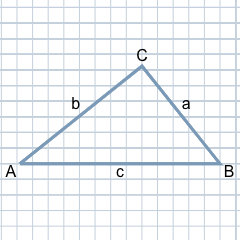Before we go into the calculations of right triangles in more detail, here is a short definition and a description of the special terms in the right triangle.
A triangle is defined by three points in the plane that do not lie on a straight line. These three points are the corners of the triangle. Each connecting line between two corners is a side of the triangle. In the plane, the triangle thus delimits a surface.
The right triangle differs from a general triangle in that one of the three angles is a right angle, i.e., a 90-degree angle. In the illustration shown here, the right angle can be seen at the top of corner C. It is denoted by the third Greek letter γ (gamma), while the angles at corner A are denoted by α (alpha) and at corner b by β (beta).
As usual, the corners are marked clockwise with the capital letters A, B and C and the sides opposite the corners are marked with the corresponding lower case letters a, b and c.
What are cathets?
In a right-angled triangle, the two sides that enclose the right angle are called the cathetes. Since the right angle in the illustration is at corner C, i.e., γ, the catheti are the two sides a and b that enclose it.
What are the adjacent and opposite catheti?
Depending on the angle under consideration, the two catheti are also called the adjacent and opposite catheti. If we look at the non-right angle α at corner A in the illustration, side b is the adjacent cathetus to a (lies at the angle α to be examined ). The second cathetus a, which lies opposite the angle α, is the opposite cathetus to a. If, on the other hand, we look at the second non-rectangular angle β at corner B, the more precise designation of the two catheti is reversed: the adjacent catheti to β is a and the opposite catheti to β is the opposite catheti b.
What is the hypotenuse?
While the cathetus are the two enclosing sides of the right angle in a right triangle, the hypotenuse is the side opposite the right angle. If the right angle is at point C, as shown in the illustration, the opposite side c is the hypotenuse. Since the right angle is always the largest angle in a right triangle, the hypotenuse is also always the longest side in a right triangle.
Introduction to the Calculation of Right Triangles
In general, one can unambiguously determine a triangle, among other things, exactly when an angle and the two enclosing sides of this angle are known. Therefore, it is sufficient to calculate a right triangle if only the two catheti, i.e., the sides enclosing the right angle, are known.
But the right angle itself also ensures that some formulas and calculation methods for the calculation of right triangles are much simpler than in the general triangle. For example, in the figure above, the height of side a is exactly equal to the length of side b and vice versa. This means that the height of one side is the length of the other side. In the general triangle, however, trigonometric functions must be used to calculate these heights.
In the following example, we will show you how to calculate a right triangle where the two catheti are known. Using these two given values, the other properties of the right-angled triangle can now be clearly determined step by step.
Example
Given the cathetus a = 4 in and the cathetus b = 5 in. Since it is a right triangle, the angle γ is already known to be 90 degrees.
Explanation
The missing side c, the perimeter and the area of the right triangle, the remaining two angles α and β, as well as the heights of all three sides of the right triangle, are sought.
You can change these values in the Right Triangle Calculator after selecting 'Two catheti for a right triangle' under ‘Which values are given?’ The calculator then calculates – as in the following calculations – all the values sought for the triangle and also outputs a graphical result of the calculated triangle.
Given a right triangle, the two known catheti (here a and b) enclose the right angle. Therefore, the formula
Formula for area of a right triangle
A = ½ × a × b
Inserting the existing values for the catheti
If you insert the values for the catheti, you get
A = ½ × 4 × 5 = 10 in²
Solution
The area A of the right triangle is 10 in².
Because of the right angle between the two known sides, the formula used is a simplification of the area formula for general triangles, which here in the calculator is used under 'Two sides with an included angle'.
The area formula for a right triangle can be illustrated by duplicating the right triangle and placing the two triangles together at their longest side, the hypotenuse, so that a rectangle is formed. This rectangle has area a × b (cathetus a times cathetus b). Thus, before duplication, the triangle has exactly half the area, i.e., ½ × a × b.
How is the missing side in the right triangle calculated?
With the given quantities for the two cathets a and b and for the right angle γ, the length of the still unknown third side c, i.e., the hypotenuse, can be calculated using the Pythagorean theorem.
.
Formula: Pythagorean theorem
a² + b² = c²
when converted to c
c = a² + b²
Inserting the existing values
By inserting the values for the catheti a = 4 and b = 5, we get
c = 4² + 5² ≈ 6.4
Solution
The hypotenuse, i.e., the missing third side c, has a length of about 6.4 in.
How is the perimeter of a right triangle calculated?
Using the given lengths for the two catheti, sides a and b, as well as the length of the hypotenuse, i.e., the side c, calculated in the meantime, the perimeter of the triangle can be determined as follows:
Formula: Perimeter P of a right triangle
The perimeter of each triangle is the sum of the lengths of all three sides a, b and c.
P = a + b + c
Inserting the existing values
Inserting the given values a = 4 and b = 5 and the already calculated value for c = 6.4, we get
How are the missing angles in the right triangle calculated?
Calculation of angle α
First, we calculate angle α: The two known catheti are the sides a and b. The angle α is at the cathetus b and opposite the cathetus a of the triangle. So, it has the adjacent side b = 5 in and the opposite side a = 4 in.
Formula for calculating the angle α in a right triangle
tan α = opposite cathetus α / adjacent α = a / b
If you convert the formula into α, you get the inverse function of the tangent, the arc tangent (arctan)
α = arctan (a / b)
Inserting the existing values
Inserting the values for the opposite cathetus a = 4 and the adjacent cathetus b = 5, we obtain
α = arctan (4 / 5) = 0.67474 rad
Intermediate solution
The angle α of the triangle is 0.67474 rad.
Here, we first calculated the radian of the angle α abbreviated as 'rad'. With the help of a calculator, the result can also be immediately converted into degrees. In this case, we perform the conversion step by step: The radian is converted to degrees using the formula
Formula: Conversion from radian to degree
α° = α rad × 180 / π
If one substitutes the intermediate result α rad, one obtains
α° = 0.67474 rad × 180 / 3.14 ≈ 38.66°
Solution
The angle α of the triangle is 38.66°.
Calculation of angle β
Now that the angle α has been calculated and the right angle γ with 90° is given anyway, the remaining angle β can be calculated. The sum of angles can be used for this.
Formula: Angle sum theorem
The sum of the three interior angles α, β and γ in a triangle is always 180 degrees.
α° + β° + γ° = 180°
If one converts the angle sum theorem to β, one obtains
β° = 180° − α° − γ°
Inserting the existing values
If one inserts the already calculated angle for α as well as the given angle γ, one obtains
How are the heights in a right triangle calculated?
Height of a and b
In a right-angled triangle, the height of side a is exactly the same as the length of the other side, i.e., side b. This is because side b, as a side, is at a right angle, i.e., perpendicular to a, and leads to the point A of the triangle opposite side a.
Analogously, the height of the cathetus b is equal to the length of a.
Formula for height of a in a right triangle
The height of cathetus a is equal to the length of the second cathetus b
ha = b
Formula for height of b in a right triangle
The height of cathetus b is equal to the length of the second cathetus a
hb = a
Solution
The height of a, i.e. ha is 5 in and the height of b is 4 in
Height of c
To calculate the height of the hypotenuse c, the following formula can now be used:
Formula for height of hypotenuse c in a right triangle
hc = a × sin β
Inserting the existing values
Inserting the known values for a = 4 in and for β = 51.34°, we obtain
Before we go into the calculations of right triangles in more detail, here is a short definition and a description of the special terms in the right triangle.