Comparé aux triangles généraux, un triangle équilatéral est une forme particulière de triangle car il a trois côtés exactement de la même longueur. Dans la section suivante, nous utiliserons un exemple avec une longueur de côté donnée pour calculer l'aire, le périmètre, les angles et les hauteurs du triangle équilatéral. Pour ce faire, nous utiliserons les formules et les règles de calcul qui ont été simplifiées spécifiquement pour les triangles équilatéraux.
Ad
Sur la page de notre calculateur de triangle, vous trouverez beaucoup d'informations sur le calcul non seulement des triangles équilatéraux mais aussi des triangles généraux. Alternativement, rendez-vous sur nos guides consacrés à l''aire d'un triangle' et aux 'triangles rectangles'.
Avant d'entrer plus en détail dans le calcul des triangles équilatéraux, voici une brève définition du triangle équilatéral.
Fondamentalement, un triangle est défini par trois points dans le plan qui ne se trouvent pas sur une ligne droite. Les trois points forment les coins du triangle. Chaque ligne de connexion entre deux de ces coins est un côté du triangle. Dans le plan, le triangle délimite donc une surface.
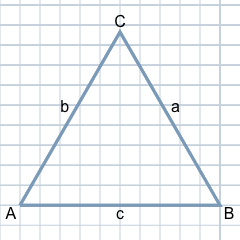
La particularité du triangle équilatéral par rapport au triangle général est que les trois côtés du triangle ont la même longueur, comme l'illustre la figure illustrée ici.
Par défaut, les coins dans le sens des aiguilles d'une montre sont étiquetés avec les lettres majuscules A, B, C. Les côtés opposés à ces coins reçoivent les lettres minuscules correspondantes a, b et c. Dans le cas d'un triangle équilatéral, les trois côtés sont généralement étiquetés a.
Les triangles équilatéraux ne diffèrent des triangles généraux que par le fait que les trois côtés ont la même longueur. Fondamentalement, un triangle peut être déterminé sans ambiguïté si les trois côtés a, b et c sont connus. Par conséquent, cela est suffisant pour calculer un triangle équilatéral si un seul côté est connu.
Cependant, dans le cas du triangle équilatéral de côté a donné, des calculs plus simples sont également possibles. Par exemple, les trois angles du triangle équilatéral sont également toujours égaux et s'élèvent toujours à 60 degrés. De même, le calcul de l'aire d'un triangle équilatéral suit une formule plus simple que, par exemple, dans le cas du triangle général à trois côtés donnés a, b et c, comme nous le verrons ci-dessous.
Ci-dessous, nous montrons un exemple de calcul d'un triangle équilatéral dont la longueur de côté a est connue. En utilisant cette valeur donnée, les autres propriétés du triangle équilatéral peuvent maintenant être clairement déterminées étape par étape.
Exemple
Soit la longueur du côté a = 5 cm. Comme il s'agit d'un triangle équilatéral, la valeur des trois côtés est déjà connue.
Explication
We are looking for the area, the perimeter, the angles and the heights of all three sides of the equilateral triangle.
Nous recherchons l'aire, le périmètre, les angles et les hauteurs des trois côtés du triangle équilatéral.
Vous pouvez entrer la valeur donnée pour le côté a dans le calculateur de triangle équilatéral après avoir sélectionné "Un côté pour un triangle équilatéral" sous "Quelles valeurs sont données ?". Le calculateur calculera alors, comme dans les calculs suivants, toutes les valeurs recherchées pour le triangle et affichera également un résultat graphique du triangle calculé.
Comment calcule-t-on l'aire d'un triangle équilatéral ?
Dans un triangle équilatéral, comme son nom le laisser deviner, les trois côtés sont de longueur égale. Par conséquent, la formule simplifiée suivante s'applique à l'aire du triangle équilatéral, où a est la longueur de l'un des côtés
Formule pour l'aire d'un triangle équilatéral
A = 3 / 4 × a²
Insertion de la valeur existante pour la longueur de la page
Comment sont calculées les hauteurs dans le triangle équilatéral ?
Pour calculer la hauteur de a dans le triangle équilatéral, la formule suivante peut être utilisée à la place de la formule plus compliquée pour les triangles généraux :
Formule pour la hauteur de a dans le triangle équilatéral
ha = 3 / 2 × a
Insertion des valeurs existantes
En substituant la valeur connue à a = 5 cm, on obtient
ha = 3 / 2 × 5 ≈ 4,33
Solution
La hauteur de a, c'est-à-dire ha est de 4,33 cm.
Les côtés b et c étant exactement aussi longs que a, leurs hauteurs sont également identiques à a.
La page de la catégorie "Triangle" a été modifié pour la dernière fois par Michael Mühl le 20.02.2023. Par ailleurs, cette page est revue en permanence par les services d'édition et correspond à l'état actuel.
Changements dans la catégorie "Triangle"
12.11.2022: Publication d'un article Calcul des triangles équilatéraux.
12.11.2022: Publication d'un article sur Aire d'un triangle et sur
Triangles rectangles.
12.11.2022: Publication du Calculer le triangle ainsi que les textes correspondants.
Révision éditoriale de cette page
Notez notre article en un seul clic
(étoile gauche pitoyable - étoile droite très bien)
5.0
étoiles avec
1
évaluations
51Calculer un triangle équilatéral
Avant d'entrer plus en détail dans le calcul des triangles équilatéraux, voici une brève définition du triangle équilatéral.