En comparación con los triángulos generales, el triángulo equilátero es un tipo especial de triángulo porque tiene los tres lados exactamente iguales. En el siguiente apartado, utilizaremos un ejemplo con una longitud de lado dada para calcular el área, el perímetro, los ángulos y las alturas del triángulo equilátero. Para ello, utilizaremos las fórmulas y reglas de cálculo simplificadas específicas para este tipo de triángulos.
Antes de profundizar en el cálculo de los triángulos equiláteros, le ofrecemos una breve definición.
Básicamente, un triángulo está definido por tres puntos en el plano que no se encuentran en una línea recta. Estos tres puntos forman los vértices del triángulo. Cada línea de unión entre dos de esos vértices es un lado. Por tanto, el triángulo delimita así una superficie en el plano.
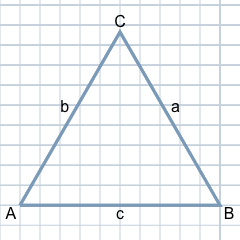
La particularidad del triángulo equilátero respecto al triángulo general es que sus tres lados tienen la misma longitud, como lo ilustra la figura.
Los vértices suelen nombrarse en el sentido de las agujas del reloj con las letras mayúsculas A, B, C. Los lados opuestos a estos vértices reciben los correspondientes nombres de a, b y c con letras minúsculas. En el caso de los triángulos equiláteros, los tres lados se suelen denominar con la letra a.
Los triángulos equiláteros se diferencian de los triángulos generales solo en que sus tres lados tienen la misma longitud. Básicamente, un triángulo puede determinarse de forma inequívoca si se conocen los tres lados (a, b y c); por lo tanto, se puede calcular un triángulo equilátero con uno solo de sus lados.
Sin embargo, en el caso del triángulo equilátero con un lado a definido, también es posible realizar cálculos más sencillos. Por ejemplo, los tres ángulos del triángulo equilátero también son siempre iguales y siempre suman 60 grados. Asimismo, el cálculo del área de un triángulo equilátero requiere una fórmula más sencilla que, por ejemplo, la del triángulo general con tres lados dados a, b y c, como veremos a continuación.
A continuación mostramos un ejemplo de cálculo de un triángulo equilátero del que se conoce la longitud de su lado a. A partir de este valor, se pueden determinar claramente, paso a paso, las demás propiedades del mismo.
Ejemplo
Dada la longitud del lado a = 5 cm. Como se trata de un triángulo equilátero, ya se conoce el valor de los tres lados.
Explicación
Buscamos el área, el perímetro, los ángulos y las alturas de los tres lados del triángulo equilátero.
Puede introducir el valor conocido para el lado a en la calculadora de triángulos equiláteros tras seleccionar "Un lado de un triángulo equilátero" en "¿Qué valores se dan?". La calculadora mostrará todos los valores buscados y también un gráfico del triángulo calculado.
¿Cómo se calcula el área de un triángulo equilátero?
En un triángulo equilátero, como su nombre lo indica, los tres lados tienen la misma longitud. Por lo tanto, para calcular su area (donde a es la longitud de uno de los lados), se aplica la siguiente fórmula simplificada.
Fórmula del área de un triángulo equilátero
A = 3 / 4 × a²
Insertar el valor existente para la longitud del lado
¿Cómo se calcula el perímetro de un triángulo equilátero?
Utilizando la longitud dada para uno de los lados y, por tanto, de los tres lados, el perímetro del triángulo puede determinarse de la siguiente manera:
Fórmula: Perímetro (P) de un triángulo equilátero
El perímetro de cada triángulo es la suma de las longitudes de sus tres lados a, b y c.
P = a + b + c
Insertar el valor existente
Si insertamos el valor dado a = 5, que es válido para todos los lados, obtenemos
P = 5 + 5 + 5 = 15
Solución
El perímetro del triángulo equilátero es de 15 cm.
¿Cómo se calculan las alturas del triángulo equilátero?
Para calcular la altura de a en el triángulo equilátero, se puede utilizar la siguiente fórmula en lugar de la fórmula más complicada de los triángulos generales:
Fórmula para la altura de a en el triángulo equilátero
ha = 3 / 2 × a
Insertar el valor existente
Sustituyendo el valor conocido de a = 5 cm, obtenemos
ha = 3 / 2 × 5 ≈ 4,33
Solución
La altura de a, es decir, ha, es de 4,33 cm.
Como los lados b y c son exactamente iguales que a, sus alturas son también idénticas
Antes de profundizar en el cálculo de los triángulos equiláteros, le ofrecemos una breve definición.
Básicamente, un triángulo está definido por tres puntos en el plano que no se encuentran en una línea recta. Estos tres puntos forman los vértices del triángulo. Cada línea de unión entre dos de esos vértices es un lado. Por tanto, el triángulo delimita así una superficie en el plano.