Un triangle rectangle est une forme particulière de triangle par rapport aux triangles généraux car, comme son nom l'indique, il possède un angle droit ou un angle de 90 degrés. Dans la section suivante, nous utiliserons des exemples pour calculer toutes les valeurs importantes du triangle rectangle en utilisant les formules spéciales et les règles de calcul pour les triangles rectangles.
Ad
Sur la page de notre calculateur de triangle, vous trouverez de nombreuses informations sur le calcul non seulement des triangles rectangles, mais également des triangles généraux. Alternativement, rendez-vous sur nos guides consacrés à l''aire d'un triangle' et aux 'triangles équilatéraux'.
Avant d'entrer plus en détail dans les calculs des triangles rectangles, voici une courte définition et une description des termes spéciaux du triangle rectangle.
Un triangle est défini par trois points dans le plan qui ne se trouvent pas sur une ligne droite. Ces trois points sont les coins du triangle. Chaque ligne de connexion entre deux coins est un côté du triangle. Dans le plan, le triangle délimite ainsi une surface.
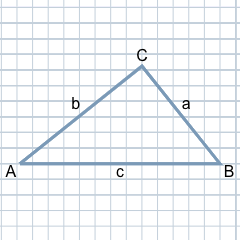
Le triangle rectangle diffère d'un triangle général en ce que l'un des trois angles est un angle droit, c'est-à-dire un angle de 90 degrés. Dans l'illustration montrée ici, l'angle droit est visible en haut du coin C. Il est désigné par la troisième lettre grecque γ (gamma), tandis que les angles au coin A sont désignés par α (alpha) et au coin b par β (bêta).
Comme d'habitude, les coins sont marqués dans le sens des aiguilles d'une montre avec les lettres majuscules A, B et C et les côtés opposés aux coins sont marqués avec les lettres minuscules correspondantes a, b et c.
Que sont les cathètes ?
Dans un triangle rectangle, les deux côtés qui entourent l'angle droit sont appelés les cathètes. Comme l'angle droit de l'illustration est au coin C, c'est-à-dire γ, les cathètes sont les deux côtés a et b qui l'entourent.
Quelles sont les cathètes adjacents et opposés ?
Selon l'angle considéré, les deux cathètes sont également appelés cathètes adjacent et opposé. Si nous regardons l'angle α non droit au coin A dans l'illustration, le côté b est le cathète adjacent à a (se trouve à l'angle α à examiner). Le deuxième cathète a, qui se trouve à l'opposé de l'angle α, est le cathète opposé à a. Si, au contraire, on regarde le deuxième angle non rectangulaire β au coin B, la désignation plus précise des deux cathètes est inversée : le cathète adjacent à β est a et le cathète opposé à β est le cathète opposé b.
Qu'est-ce que l'hypoténuse ?
Alors que les cathètes sont les deux côtés englobants de l'angle droit dans un triangle rectangle, l'hypoténuse est le côté opposé à l'angle droit. Si l'angle droit est au point C, comme le montre l'illustration, le côté opposé c est l'hypoténuse. Puisque l'angle droit est toujours le plus grand angle d'un triangle rectangle, l'hypoténuse est également toujours le côté le plus long d'un triangle rectangle.
En général, on peut déterminer sans ambiguïté un triangle, entre autres, exactement lorsqu'un angle et les deux côtés englobants de cet angle sont connus. Cela est donc suffisant pour calculer un triangle rectangle si seulement les deux cathètes, c'est-à-dire les côtés entourant l'angle droit, sont connus.
Mais l'angle droit lui-même garantit également que certaines formules et méthodes de calcul pour le calcul des triangles rectangles sont beaucoup plus simples que dans le triangle général. Par exemple, dans la figure ci-dessus, la hauteur du côté a est exactement égale à la longueur du côté b et vice versa. Cela signifie que la hauteur d'un côté est la longueur de l'autre côté. Dans le triangle général, cependant, des fonctions trigonométriques doivent être utilisées pour calculer ces hauteurs.
Dans l'exemple suivant, nous allons vous montrer comment calculer un triangle rectangle où les deux cathètes sont connus. En utilisant ces deux valeurs données, les autres propriétés du triangle rectangle peuvent maintenant être clairement déterminées étape par étape.
Exemple
Soit le cathète a = 4 cm et le cathète b = 5 cm. Puisqu'il s'agit d'un triangle rectangle, l'angle ? est déjà connu pour être de 90 degrés.
Explication
Le côté manquant c, le périmètre et l'aire du triangle rectangle, les deux angles restants α et β, ainsi que les hauteurs des trois côtés du triangle rectangle, sont recherchées.
Vous pouvez modifier ces valeurs dans le calculateur de triangle rectangle après avoir sélectionné "Deux cathètes pour un triangle rectangle" sous "Quelles valeurs sont données ?" Le calculateur calcule ensuite, comme dans les calculs suivants, toutes les valeurs recherchées pour le triangle et affiche également un résultat graphique du triangle calculé.
Comment l'aire d'un triangle rectangle est-elle calculée ?
Dans un triangle rectangle, les deux cathètes connues (ici a et b) renferment l'angle droit. Par conséquent, la formule
Formule pour l'aire d'un triangle rectangle
A = ½ × a × b
Insertion des valeurs existantes pour le cathète
Si vous insérez les valeurs des cathètes, vous obtenez
A = ½ × 4 × 5 = 10 cm²
Solution
L'aire A du triangle rectangle est de 10 cm².
En raison de l'angle droit entre les deux côtés connus, la formule utilisée est une simplification de la formule d'aire des triangles généraux, qui est utilisée ici dans le calculateur sous "Deux côtés avec un angle inclus".
La formule de l'aire d'un triangle rectangle peut être illustrée en dupliquant le triangle rectangle et en plaçant les deux triangles ensemble sur leur côté le plus long, l'hypoténuse, de manière à former un rectangle. Ce rectangle a l'aire a × b (cathète a fois cathète b). Ainsi, avant duplication, le triangle a exactement la moitié de l'aire, c'est-à-dire ½ × a × b.
Comment est calculé le côté manquant dans le triangle rectangle ?
Avec les quantités données pour les deux cathètes a et b et pour l'angle droit ?, la longueur du troisième côté c encore inconnu, c'est-à-dire l'hypoténuse, peut être calculée à l'aide du Théorème de Pythagore.
Formule : Théorème de Pythagore
a² + b² = c²
lorsqu'il est converti en c
c = a² + b²
Insertion des valeurs existantes
En insérant les valeurs des cathètes a = 4 et b = 5, on obtient
c = 4² + 5² ≈ 6.4
Solution
L'hypoténuse, c'est-à-dire le troisième côté manquant c, a une longueur d'environ 6,4 cm.
Comment le périmètre d'un triangle rectangle est-il calculé ?
En utilisant les longueurs données pour les deux cathètes, les côtés a et b, ainsi que la longueur de l'hypoténuse, c'est-à-dire le côté c, calculée entre-temps, le périmètre du triangle peut être déterminé comme suit :
Formule : périmètre P d'un triangle rectangle
Le périmètre de chaque triangle est la somme des longueurs des trois côtés a, b et c.
P = a + b + c
Insertion des valeurs existantes
En insérant les valeurs données a = 4 et b = 5 et la valeur déjà calculée pour c = 6,4, on obtient
U = 4 + 6 + 6,4 = 16,4
Solution
Le périmètre du triangle rectangle est de 16,4 cm.
Comment sont calculés les angles manquants dans le triangle rectangle ?
Calcul de l'angle α
D'abord, nous calculons l'angle α : les deux cathètes connus sont les côtés a et b. L'angle α est à la cathète b et opposée à la cathète a du triangle. Ainsi, il a le côté adjacent b = 5 cm et le côté opposé a = 4 cm.
Formule de calcul de l'angle α dans un triangle rectangle
tan α = cathète opposé α / adjacent α = a / b
Si vous convertissez la formule en α, vous obtenez la fonction inverse de la tangente, l'arc tangente (arctan)
α = arctan (a / b)
Insertion des valeurs existantes
En insérant les valeurs pour le cathète opposé a = 4 et le cathète adjacent b = 5, on obtient
α = arctan (4 / 5) = 0,67474 rad
Solution intermédiaire
L'angle α du triangle est de 0,67474 rad.
Ici, nous avons d'abord calculé le radian de l'angle ?, abrégé en "rad". À l'aide d'un calculateur, le résultat peut également être immédiatement converti en degrés. Dans ce cas, nous effectuons la conversion étape par étape : le radian est converti en degrés en utilisant la formule
Formule : conversion du radian en degré
α° = α rad × 180 / π
Si l'on substitue le résultat intermédiaire α rad, on obtient
α° = 0,67474 rad × 180 / 3,14 ≈ 38,66°
Solution
L'angle α du triangle est de 38,66°.
Calcul de l'angle β
Maintenant que l'angle α a été calculé et que l'angle droit γ à 90° est donné de toute façon, l'angle restant β peut être calculé. La somme des angles peut être utilisée pour cela.
Formule : théorème de somme des angles
La somme des trois angles intérieurs α, β et γ dans un triangle est toujours de 180 degrés.
α° + β° + γ° = 180°
Si l'on convertit le théorème de la somme des angles en β, on obtient
β° = 180° − α° − γ°
Insertion des valeurs existantes
Si l'on insère l'angle déjà calculé pour α ainsi que l'angle donné γ, on obtient
Comment sont calculées les hauteurs d'un triangle rectangle ?
Hauteur de a et b
Dans un triangle rectangle, la hauteur du côté a est exactement la même que la longueur de l'autre côté, c'est-à-dire le côté b. En effet, le côté b, en tant que côté, est à angle droit, c'est-à-dire perpendiculaire à a, et mène au point A du triangle opposé au côté a.
De manière analogue, la hauteur du cathète b est égale à la longueur de a.
Formule pour la hauteur de a dans un triangle rectangle
La hauteur du cathète a est égale à la longueur du deuxième cathète b
ha = b
Formule pour la hauteur de b dans un triangle rectangle
La hauteur du cathète b est égale à la longueur du deuxième cathète a
hb = a
Solution
La hauteur de a, c'est-à-dire ha est de 5 cm et la hauteur de b est de 4 cm
Hauteur de c
Pour calculer la hauteur de l'hypoténuse c, la formule suivante peut maintenant être utilisée :
Formule pour la hauteur de l'hypoténuse c dans un triangle rectangle
hc = a × sin β
Insertion des valeurs existantes
En additionnant les valeurs connues pour a = 4 cm et pour β = 51,34°, on obtient
Le triangle rectangle calculé de cette manière avec des côtés donnés a = 4 cm et b = 5 cm peut être dessiné en utilisant toutes les valeurs calculées comme suit :
Résultat graphique
1 case équivaut à 0,5 unité (comme indiqué dans le livre d'arithmétique)
Avant d'entrer plus en détail dans les calculs des triangles rectangles, voici une courte définition et une description des termes spéciaux du triangle rectangle.