Um triângulo retângulo é um tipo especial de triângulo quando comparado com triângulos gerais porque, tal como o nome sugere, tem um ângulo retângulo, isto é, um ângulo de 90 graus. Na secção seguinte, utilizaremos exemplos para calcular todos os valores importantes do triângulo retângulo utilizando as fórmulas especiais e regras de cálculo para os triângulos retângulos.
Ad
Na página da nossa Calculadora de triângulo encontrará muitas informações sobre o cálculo, não só de triângulos retângulos, mas também de triângulos gerais. Alternativamente, visite os nossos guias sobre os tópicos "Área de um triângulo" e "Triângulos equiláteros".
Antes de entrarmos nos cálculos dos triângulos retângulos, mais detalhadamente, segue uma breve definição e uma descrição dos termos especiais do triângulo retângulo.
Um triângulo é definido por três pontos no plano que não se encontram numa linha reta. Estes três pontos são os cantos do triângulo. Cada linha de ligação entre dois cantos é um lado do triângulo. No plano, o triângulo delimita uma superfície.
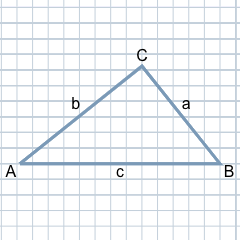
A diferença entre um triângulo retângulo e um triângulo geral é que um dos três ângulos é um ângulo reto, ou seja, um ângulo de 90 graus. Na ilustração aqui exibida, o ângulo reto pode ser visto no topo do canto C. Este é identificado pela terceira letra grega ? (gama), enquanto o ângulo no canto A é identificado com ? (alfa) e no canto B por ? (beta).
Como é habitual, os cantos são assinalados no sentido horário com as letras maiúsculas A, B e C e os lados opostos aos cantos são assinalados com as letras minúsculas a, b e c correspondentes.s.
O que são os catetos?
Num triângulo retângulo, os dois lados adjacentes ao ângulo reto designam-se por catetos. Dado que o ângulo reto na figura é o canto C, ou seja, γ, os catetos são os dois lados adjacentes a e b.
O que são o cateto adjacente e o cateto oposto?
Consoante o ângulo em consideração, os dois catetos também são designados por cateto adjacente e cateto oposto. Se olharmos para o ângulo não retângulo α no canto A da figura, o lado b é o cateto adjacente a a (encontra-se no ângulo α a ser examinado). O segundo cateto a, que se encontra oposto ao ângulo α, é o cateto oposto a a. Se, por outro lado, olharmos para o segundo ângulo não retângulo β no canto B, a designação mais precisa dos dois catetos inverte-se: o cateto adjacente a β é a e o cateto oposto a β é o cateto oposto b.
O que é a hipotenusa?
Embora os catetos sejam os dois lados adjacentes ao ângulo reto num triângulo retângulo, a hipotenusa é o lado oposto do ângulo reto. Se o ângulo reto está no ponto C, conforme a figura, o lado oposto c é a hipotenusa. Dado que o ângulo reto é sempre o maior ângulo num triângulo retângulo, a hipotenusa também é sempre o maior lado num triângulo retângulo.
Em termos gerais, podemos determinar de forma inequívoca um triângulo, entre outros fatores, exatamente quando um canto e os dois lados adjacentes a este ângulo são conhecidos. Por conseguinte, é suficiente calcular um triângulo retângulo se apenas os dois catetos, isto é, os lados que encerram o ângulo reto, são conhecidos.
Mas o ângulo reto em si também assegura que algumas fórmulas e métodos de cálculo para calcular os triângulos retos são muito mais simples do que no triângulo geral. Por exemplo, na figura supra, a altura do lado a é exatamente igual ao comprimento do lado b e vice-versa. Isto significa que a altura de um lado é o comprimento do outro lado. No triângulo geral, contudo, as funções trigonométricas devem ser utilizadas para calcular estas alturas.
No exemplo seguinte, iremos mostrar-lhe como calcular um triângulo retângulo onde os dois catetos são conhecidos. Utilizando estes dois valores conhecidos, as outras propriedades do triângulo retângulo podem agora ser claramente determinadas, passo a passo.
Exemplo
Considerando que o cateto a = 4 cm e o cateto b = 5 cm. Dado que é um triângulo retângulo, já se sabe que o ângulo reto é de 90 graus.
Explicação
Procura-se determinar o lado c em falta, o perímetro e a área do triângulo retângulo, os dois ângulos restantes, bem como as alturas de todos os três lados do triângulo retângulo.
Pode alterar estes valores na Calculadora de triângulo retângulo após selecionar "Dois catetos para um triângulo retângulo" em "Que valores são conhecidos?" De seguida, a calculadora calcula – tal como nos cálculos seguintes – todos os valores estabelecidos para o triângulo e também revela um resultado gráfico do triângulo calculado.
Num triângulo retângulo, os dois catetos conhecidos (aqui a e b) encerram o ângulo reto. Por conseguinte:
Fórmula para a área de um triângulo retângulo
A = ½ × a × b
Inserindo os valores existentes para os catetos
Se inserir os valores para os catetos, obtém
A = ½ × 4 × 5 = 10 cm²
Solução
A área A do triângulo retângulo é 10 cm².
Devido ao ângulo reto entre os dois lados conhecidos, a fórmula utilizada é uma simplificação da fórmula da área para os triângulos gerais, que, aqui na calculadora, é utilizada em "Dois lados com um ângulo incluído".
A fórmula da área para um triângulo retângulo pode ser ilustrada duplicando o triângulo retângulo e colocando os dois triângulos em conjunto pelo seu lado mais comprido, a hipotenusa, de modo a formar assim um retângulo. Este retângulo tem área a x b (cateto a vezes cateto b). Assim sendo, antes da duplicação, o triângulo tem exatamente metade da área, isto é,
½ × a × b.
Como é calculado o lado em falta do triângulo retângulo?
Com os valores dados para os dois catetos a e b e para o ângulo reto, o comprimento do terceiro lado ainda desconhecido c, hipotenusa, pode ser calculado utilizando o teorema de Pitágoras.
.
Fórmula: teorema de Pitágoras
a² + b² = c²
quando convertido para c
c = a² + b²
Inserindo os valores existentes
Inserindo os valores para os catetos a = 4 e b = 5, obtemos
c = 4² + 5² ≈ 6,4
Solução
A hipotenusa, isto é, o terceiro lado em falta c, tem um comprimento de 6,4 cm.
Como é calculado o perímetro de um triângulo retângulo?
Utilizando os comprimentos dados para os dois catetos, os lados a e b, bem como o comprimento da hipotenusa, ou seja, o lado c, calculados entretanto, o perímetro do triângulo pode ser determinado da seguinte forma:
Fórmula: perímetro P de um triângulo retângulo
O perímetro de cada triângulo é a soma dos comprimentos de todos os três lados a, b e c.
P = a + b + c
Inserindo os valores existentes
Inserindo os valores dados a = 4 e b = 5 e o valor já calculado para c = 6,4, obtemos
Como são calculados os ângulos em falta do triângulo retângulo?
Cálculo do ângulo α
Primeiro, calculamos o ângulo α: os dois catetos conhecidos são os lados a e b. O ângulo α está no cateto b e oposto ao cateto a do triângulo. Assim sendo, tem o lado adjacente b = 5 e o lado oposto a = 4 cm.
Fórmula para calcular o ângulo α num triângulo retângulo
tan α = cateto oposto ? / adjacente α = a / b
Se converter a fórmula em α, obtém a função inversa da tangente, o arco tangente (arctan)
α = arctan (a / b)
Inserindo os valores existentes
Inserindo os valores para o cateto oposto a = 4 e o cateto adjacente b = 5, obtemos
α = arctan (4 / 5) = 0,67474 rad
Solução intermédia
O ângulo α do triângulo é 0,67474 rad.
Aqui, calculámos primeiro o radiano do ângulo α, abreviados como "rad". Com a ajuda de uma calculadora, o resultado também pode ser imediatamente convertido para graus. Neste caso, realizamos a conversão passo a passo: o radiano é convertido em graus utilizando:
Fórmula: conversão de radianos para graus
α° = α rad × 180 / π
Se substituir o resultado intermédio α rad, obtemos
α° = 0,67474 rad × 180 / 3,14 ≈ 38,66°
Solução
O ângulo α do triângulo é 38,66°.
Cálculo do ângulo β
Agora que o ângulo α já foi calculado e o ângulo reto γ com 90° já é mais do que conhecido, podemos calcular o ângulo β em falta. A soma dos ângulos pode ser utilizada para isto.
Fórmula: teorema da soma dos ângulos
A soma dos três ângulos interiores α, β e γ de um triângulo é sempre 180 graus.
α° + β° + γ° = 180°
Se convertermos o teorema da soma dos ângulos para β, obtemos
β° = 180° − α° − γ°
Inserindo os valores existentes
Se inserirmos o ângulo já calculado para α, bem como o ângulo ? dado, obtemos
Como são calculadas as alturas num triângulo retângulo?
Altura de a e de b
Num triângulo retângulo, a altura do lado a é exatamente igual ao comprimento do outro lado, ou seja, o lado b. Isto deve-se ao facto de o lado b, enquanto lado, se encontrar num ângulo reto, ou seja, perpendicular a a, indo até ao ponto A do lado oposto a do triângulo.
Analogamente, a altura do cateto b é igual ao comprimento de a.
Fórmula para a altura de a num triângulo retângulo
A altura do cateto a é igual ao comprimento do segundo cateto b
ha = b
Fórmula para a altura de b num triângulo retângulo
A altura do cateto b é igual ao comprimento do segundo cateto a
hb = a
Solução
A altura de a, ou ha é 5 cm e a altura de b é 4 cm
Altura de c
Para calcular a altura da hipotenusa c, a seguinte fórmula pode agora ser utilizada:
Fórmula para a altura da hipotenusa c num triângulo retângulo
hc = a × sin β
Inserindo os valores existentes
Inserindo os valores conhecidos para a = 4 cm e para β = 51,34°, obtemos
Como é representado o triângulo retângulo calculado?
O triângulo retângulo calculado desta forma com os lados dados a = 4 cm e b = 5 cm pode ser desenhado utilizando todos os valores calculados da seguinte forma:
Resultado gráfico
1 quadrado equivale a 0,5 unidades (conforme demonstrado no livro aritmético)
Antes de entrarmos nos cálculos dos triângulos retângulos, mais detalhadamente, segue uma breve definição e uma descrição dos termos especiais do triângulo retângulo.