El rectángulo es un tipo especial de triángulo en comparación con los triángulos generales porque, como su nombre lo indica, tiene un ángulo de 90 grados o recto. En la siguiente sección, veremos ejemplos de cálculo de todos los valores importantes del triángulo rectángulo utilizando las fórmulas y reglas especiales para este tipo de triángulos.
En la página de nuestra Calculadora de triángulos encontrará mucha información sobre el cálculo no solo de triángulos rectángulos, sino de los triángulos en general. También puede visitar nuestras guías sobre los temas "Área de un triángulo" y "Triángulos equiláteros".
Antes de profundizar en los cálculos de los triángulos rectángulos, aquí tenemos una breve definición y una descripción de los términos especiales de estos triángulos.
Un triángulo está definido por tres puntos del plano que no se encuentran en una línea recta. Estos tres puntos son los vértices del triángulo. Cada línea de unión entre dos vértices es un lado. En el plano, el triángulo delimita una superficie.
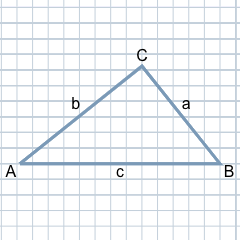
El triángulo rectángulo se diferencia del triángulo general en que uno de sus tres ángulos es recto, es decir, tiene 90 grados. En la ilustración que se muestra aquí, el ángulo recto se puede ver en la parte superior de la esquina C. Se designa con la tercera letra griega γ (gamma), mientras que el ángulo del vértice A se designa con la letra α (alfa) y el del vértice b con la letra β (beta).
Como es habitual, los vértices se señalan en el sentido de las agujas del reloj con las letras mayúsculas A, B y C, y los lados opuestos a los vértices se señalan con las correspondientes letras minúsculas a, b y c.
¿Qué son los catetos?
En un triángulo rectángulo, los dos lados que delimitan el ángulo recto se llaman catetos. Como el ángulo recto de la ilustración está en el vértice C, es decir, γ, los catetos son los lados a y b.
¿Qué son los catetos adyacentes y opuestos?
Dependiendo del ángulo considerado, los dos catetos se denominan adyacentes u opuestos. Si nos fijamos en el ángulo no recto α del vértice A de la ilustración, el lado b es el cateto adyacente a a (es contiguo al ángulo α). El segundo cateto se encuentra frente al ángulo α, es el cateto opuesto a a. Si, en cambio, nos fijamos en el segundo ángulo no recto β en el vértice B, la designación de los dos catetos se invierte: el cateto adyacente a β es a y el cateto opuesto a β es b.
¿Qué es la hipotenusa?
Mientras que los catetos son los dos lados que encierran el ángulo recto del triángulo rectángulo, la hipotenusa es el lado opuesto al mismo. Si el ángulo recto está en el punto C, como se muestra en la ilustración, el lado opuesto c es la hipotenusa. Dado que el ángulo recto es siempre el mayor de los tres, la hipotenusa es también siempre el lado más largo.
En general, se puede determinar inequívocamente un triángulo cuando se conoce uno de sus ángulos y los dos lados que lo delimitan. Por lo tanto, si solo se conocen los dos catetos, es decir, los lados que encierran el ángulo recto, bastará para calcular el triángulo rectángulo.
El ángulo recto hace que algunas fórmulas y métodos de cálculo sean mucho más sencillos que en el triángulo general. Por ejemplo, en la figura anterior, la altura del lado a es exactamente igual a la longitud del lado b y viceversa. Esto significa que la altura de un lado es igual a la longitud del otro. En el triángulo general hay que utilizar funciones trigonométricas para calcular dichas alturas.
En el siguiente ejemplo, mostraremos cómo calcular un triángulo rectángulo del que se conocen los dos catetos. A partir de estos dos valores dados se pueden determinar las demás propiedades
Ejemplo
Dado el cateto a = 4 cm y el cateto b = 5 cm. Al tratarse de un triángulo rectángulo, ya se sabe que el ángulo ? es de 90 grados.
Explicación
Se busca el lado c faltante, el perímetro, el área, las alturas de los tres lados y los dos ángulos restantes, α y β.
Se pueden cambiar estos valores en la calculadora de triángulos rectángulos después de seleccionar "Dos catetos de un triángulo rectángulo" en "¿Qué valores se dan?". La calculadora determina entonces todos los valores buscados para el triángulo y también muestra un resultado gráfico del triángulo obtenido.
¿Cómo se calcula el área de un triángulo rectángulo?
En un triángulo rectángulo, los dos catetos conocidos (aquí a y b) encierran el ángulo recto. Por lo tanto, la fórmula es
Fórmula del área de un triángulo rectángulo
A = ½ × a × b
Inserción de los valores existentes para los catetos
Si se insertan los valores de los catetos, se obtiene
A = ½ × 4 × 5 = 10 cm²
Solución
El área (A) del triángulo rectángulo es de 10 cm².
Debido al ángulo recto existente entre los dos lados conocidos, la fórmula utilizada es una simplificación de la de los triángulos generales que aquí, en la calculadora, se aplica en "Dos lados y el ángulo comprendido entre ellos".
La fórmula del área de un triángulo rectángulo puede ilustrarse duplicándolo y uniendo ambos triángulos por su lado más largo, la hipotenusa, de modo que se forme un rectángulo. Este rectángulo tiene un área a × b (cateto a por cateto b). Así, antes de la duplicación, el triángulo tenía la mitad del área, es decir, ½ × a × b.
¿Cómo se calcula el lado faltante en el triángulo rectángulo?
Con los dos catetos a y b y el ángulo recto α, se puede calcular la longitud del lado c aún desconocido, es decir, la hipotenusa, utilizando el teorema de Pitágoras.
Fórmula: teorema de Pitágoras
a² + b² = c²
cuando se convierte para c
c = a² + b²
Inserción de los valores existentes
Insertando los valores de los catetos a = 4 y b = 5, obtenemos
c = 4² + 5² ≈ 6,4
Solución
La hipotenusa, es decir, el lado c faltante, tiene una longitud de aproximadamente 6,4 cm.
¿Cómo se calcula el perímetro de un triángulo rectángulo?
Utilizando las longitudes de los catetos (los lados a y b) y la longitud calculada para la hipotenusa (el lado c), se puede determinar el perímetro del triángulo de la siguiente manera:
Fórmula: perímetro (P) de un triángulo rectángulo
El perímetro de un triángulo es la suma de las longitudes de sus tres lados: a, b y c.
P = a + b + c
Inserción de los valores existentes
Insertando los valores conocidos a = 4 y b = 5, y el valor calculado c = 6,4, obtenemos
P = 4 + 6 + 6,4 = 16,4
Solución
El perímetro del triángulo rectángulo es de 16,4 cm.
¿Cómo se calculan los ángulos faltantes en el triángulo rectángulo?
Cálculo del ángulo α
Primero, calculamos el ángulo α: los dos catetos conocidos son los lados a y b. El ángulo ? está junto al cateto b y es opuesto al cateto a; por lo tanto, b es su lado adyacente, b = 5 cm, y a es su lado opuesto, a = 4 cm.
Fórmula para calcular el ángulo α en un triángulo rectángulo
tan α = cateto opuesto α / cateto adyacente α = a / b
Si se convierte la fórmula para α, se obtiene la función inversa de la tangente, la arcotangente (arcotan)
α = arcotan (a / b)
Inserción de los valores existentes
Insertando los valores del cateto opuesto a = 4 y del cateto adyacente b = 5, obtenemos
α = arcotan (4 / 5) = 0,67474 rad
Solución intermedia
El ángulo α del triángulo es 0,67474 rad.
Aquí, primero calculamos el radián del ángulo ?, abreviado como "rad". Con la ayuda de una calculadora, se puede convertir el resultado en grados. En este caso, realizamos la conversión paso a paso; el radián se convierte en grados mediante la siguiente formula.
Fórmula: conversión de radianes a grados
α° = α rad × 180 / π
Si se sustituye el resultado intermedio α rad, se obtiene
α° = 0,67474 rad × 180 / 3,14 ≈ 38,66°
Solución
El ángulo α del triángulo es de 38,66°.
Cálculo del ángulo β
Ahora que se ha calculado el ángulo α y se conoce el ángulo recto γ de 90°, se puede calcular el ángulo β. Para ello se puede utilizar la suma de los ángulos.
Fórmula: teorema de la suma de los ángulos
La suma de los tres ángulos interiores α, β y γ de un triángulo es siempre 180 grados.
α° + β° + γ° = 180°
Si se convierte el teorema de la suma de los ángulos para β, se obtiene
β° = 180° − α° − γ°
Inserción de los valores existentes
Si se inserta el ángulo calculado α y el ángulo dado γ, se obtiene
¿Cómo se calculan las alturas en un triángulo rectángulo?
Altura de a y b
En un triángulo rectángulo, la altura del lado a es exactamente igual a la longitud del lado b. Esto se debe a que el lado b, forma parte del ángulo recto, es decir, es perpendicular a a, y conduce al vértice A, que es opuesto al lado a.
Análogamente, la altura del cateto b es igual a la longitud de a.
Fórmula para la altura de a en un triángulo rectángulo
La altura del cateto a es igual a la longitud del cateto b
ha = b
Fórmula para la altura de b en un triángulo rectángulo
La altura del cateto b es igual a la longitud del segundo a
hb = a
Solución
La altura de a (ha) es de 5 cm, y la altura de b es de 4 cm
Altura de c
Ahora se puede utilizar la siguiente fórmula para calcular la altura de la hipotenusa c:
Fórmula para la altura de la hipotenusa c en un triángulo rectángulo
hc = a × sen β
Inserción de los valores existentes
Insertando los valores conocidos a = 4 cm y β = 51,34°, obtenemos
¿Qué aspecto tiene el triángulo rectángulo calculado?
El triángulo rectángulo calculado de esta manera, con los lados dados a = 4 cm y b = 5 cm y con todos sus valores calculados se puede representar de la siguiente manera:
Resultado gráfico
1 casilla equivale a 0,5 unidades (como en el cuaderno de matemáticas)
Antes de profundizar en los cálculos de los triángulos rectángulos, aquí tenemos una breve definición y una descripción de los términos especiales de estos triángulos.