Aqui, encontrará todas as fórmulas e inúmeros exemplos para calcular a área de triângulos. São tidas em consideração as áreas tanto de triângulos gerais como de triângulos especiais, tais como os triângulos retângulos ou equiláteros. Com a calculadora para calcular a área de triângulos, pode simplesmente inserir as dimensões conhecidas de um triângulo e, desta forma, ter a área do triângulo calculada. Além de exibir a área calculada desta forma, também receberá derivações detalhadas do cálculo da área no resultado da calculadora.
Na página da nossa Calculadora de triângulo encontrará inúmeros exemplos para o cálculo de todas as características dos triângulos. Além disso, também pode visitar os nossos guias para tópicos como 'Triângulos retângulos' e 'Triângulos equiláteros'.
Índice sobre o tópico "Área de um triângulo"
Conteúdos
- Definição de um triângulo
- Identificação de um triângulo
- Área dos triângulos
- 1. Dado um lado conhecido e uma altura h associada
- 2. Dados três lados conhecidos
- 3. Dados os triângulos equiláteros com um lado conhecido
- 4. Com dois lados conhecidos e um ângulo fechado
- 5. Dados triângulos retângulos com cateto conhecido
- 6. Com um lado conhecido e dois ângulos conhecidos
- 7. Com dois lados conhecidos e um ângulo oposto no lado mais comprido
Definição de um triângulo
Antes de entrarmos no cálculo da área de um triângulo, segue uma breve definição de um triângulo e uma descrição dos termos gerais de um triângulo.
Um triângulo é definido por três pontos no plano que não se encontram numa linha reta. Estes três pontos são os cantos do triângulo. Cada linha ligada entre dois cantos é um lado do triângulo. No plano, o triângulo delimita assim uma superfície.
As propriedades importantes de um triângulo são a sua área, o comprimento dos seus três lados, o perímetro do triângulo, os ângulos que os lados formam uns com os outros e as alturas de cada lado em relação ao canto oposto.
Pode calcular facilmente a área de um triângulo e as suas outras propriedades online utilizando a calculadora para calcular a área de um triângulo. Na secção seguinte, também encontrará todas as opções para calcular a área, incluindo fórmulas de cálculo com exemplos.
Como é identificado um triângulo?
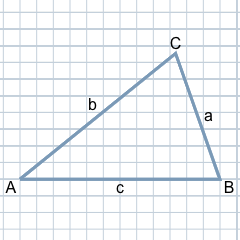
Os três cantos de um triângulo são habitualmente identificados com as letras maiúsculas A, B e C. Esta identificação é feita no sentido anti-horário e começa habitualmente com o A do canto inferior esquerdo.
Os três lados de um triângulo são designados pelas letras minúsculas a, b e c. Aqui, o lado oposto ao canto A é identificado com a letra a. Respetivamente, o lado b está oposto ao canto B e o lado c está oposto ao canto C.
Os três ângulos interiores de um triângulo são batizados utilizando as letras gregas α (alfa), β (beta) e γ (gama). Elas são colocadas nos cantos correspondentes: α pertence ao canto A, β ao B e o ângulo γ ao C.
A altura de um lado corresponde à distância perpendicular do ponto do canto oposto a este lado ou à sua extensão. Assim sendo, a altura de a (ha) corresponde à distância entre o canto A e o lado oposto a, na qual ha é perpendicular. Analogamente, são definidas a altura de b (hb) e a altura de c (hc).
Introdução à área dos triângulos
Para calcular a área de um triângulo, o comprimento de um lado em conjunto com a altura correspondente é o suficiente. Utilizando estes dois valores conhecidos, pode determinar a área do triângulo. Iremos lidar com este caso na secção seguinte em "Área de um triângulo com um lado conhecido e uma altura h correspondente".
No entanto, acontece frequentemente que o comprimento de um lado e a altura correspondente não são conhecidos. Em vez disso, outras propriedades, tais como o comprimento de todos os três lados do triângulo, são indicadas ou outras combinações de propriedades são conhecidas, as quais também permitem calcular a área. Tendo o primeiro caso mencionado como exemplo, no qual um lado da base e a altura correspondente são conhecidas, avançamos desta forma para mais seis combinações das propriedades do triângulo fornecidas de (2) a (7), segundo a base da qual a área do triângulo pode ser calculada. Já agora, estas combinações de valores conhecidos, isto é, (2) a (7), não só são adequadas para o cálculo da área do triângulo como também são adequadas para calcular a área total do triângulo utilizando as combinações. Utilizando estas combinações, todo o triângulo pode ser calculado além da área.
1. Área de triângulos com um lado conhecido e uma altura h correspondente
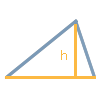Este é o "caso clássico" habitualmente ensinado primeiro nas aulas da escola. Utilizando o comprimento de uma base g e a altura h correspondente, a área do triângulo pode ser calculada com a ajuda de uma simples fórmula. Contudo, só estes dois dados não são suficientes para determinar um triângulo de forma inequívoca, por exemplo, calcular os comprimentos dos outros lados e, por conseguinte, construir o triângulo. Por outro lado, a seguinte fórmula adequa-se melhor para calcular a área total.
Exemplo
Iremos mostrar-lhe aqui como calcular a área utilizando um exemplo em que o lado a de um triângulo é a = 6 cm e a altura ha = 4 cm.
Fórmula da área para um lado base a altura dados
A = ½ × g × hg
onde A = área, g = comprimento do lado da base e h = altura em relação ao lado da base
Inserindo os valores de exemplo
Inserindo os valores a = 6 para o lado da base e a altura a = 4, obtemos
A = ½ × 6 × 4 = 12.
Solução
A área do triângulo é 12 cm².
Já agora, cada um dos três lados a, b e c, com as suas alturas h correspondentes, pode ser utilizado para calcular a área A
O respetivo lado da base e a altura devem, como é óbvio, ser indicados na mesma unidade de medida. Se, por exemplo, o lado da base for indicado em mm e a altura em polegadas, estes devem ser primeiro convertidos para uma das duas unidades de medida antes de calcular a área do triângulo. Obviamente, isto também se aplica a todos os outros cálculos da área que se sigam.
2. Área de um triângulo com três lados conhecidos
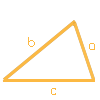Assim que todos os três lados de um triângulo forem indicados, todas as suas propriedades também podem ser calculadas. Gostaríamos, aqui, de apresentar a fórmula de Heron para calcular a área do triângulo.
Exemplo
Iremos mostrar-lhe aqui como calcular a área do triângulo com um exemplo onde os lados são a = 4 cm, b = 6 cm e c = 6 cm.
Fórmula da área (fórmula de Heron)
A = s(s − a)(s − b)(s − c)
onde s = metade da circunferência, isto é,
s = (a + b + c) / 2
Inserindo os valores existentes
Inserindo os valores a = 4, b = 6 e c = 6, primeiro obtemos s com
s = (4 + 6 + 6) / 2 = 8
Se substituirmos s = 8 na fórmula de Heron, finalmente obtemos
A = 8 × (8 − 4) × (8 − 6) × (8 − 6)) ≈ 11,31
Solução
A área do triângulo com três lados conhecidos é cerca de 11,31 cm².
3. Área de um triângulo equilátero com um lado conhecido
Se o comprimento de um lado de um triângulo equilátero é conhecido, sabemos naturalmente o comprimento de todos os três lados, porque os dois lados restantes também têm o mesmo comprimento. Assim sendo, temos finalmente um triângulo com três lados conhecidos. Agora podemos avançar com a "Área de triângulos com três lados conhecidos" utilizando a fórmula de Heron para calcular a área do triângulo. No entanto, esta fórmula é simplificada devido ao facto de que todos os três lados são de igual comprimento.
Exemplo
Mostrar-lhe-emos aqui como calcular a área utilizando um exemplo onde o triângulo equilátero tem um comprimento de lado a = 5 cm.
Fórmula da área para o triângulo equilátero
A = 3 / 4 × a²
Inserir os valores existentes
Se inserir a = 3 na fórmula, obtém
A = 3 / 4 × 5² ≈ 10,83
Solução
A área do triângulo equilátero é cerca de 10,83 cm².
4. Área de um triângulo com dois lados conhecidos e um ângulo fechado por estes
Com dois lados conhecidos e o ângulo fechado por estes, todas as propriedades e, por conseguinte, a área de um triângulo pode ser calculada.
Por exemplo, agora pode determinar primeiro a altura de um dos lados conhecidos (ou seja para lados conhecidos a e b com um ângulo γ incluído, a altura para b utilizando hb = a × sin γ) e, de seguida, conforme descrito na "Área para um triângulo com um lado conhecido e altura h associada", utilize a fórmula A = ½ × b × hb.
Aqui, no entanto, queremos primeiro calcular o terceiro lado em falta utilizando o teorema cosseno e, de seguida, conforme descrito na "Área de um triângulo com três lados conhecidos, utilize a fórmula de Heron para calcular a área do triângulo com todos os três lados conhecidos.
Exemplo
A área é calculada aqui utilizando um exemplo onde os dois lados a = 4 cm e b = 6 cm e o ângulo γ fechado por a e b é de 70 graus.
Fórmula para calcular o lado em falta (teorema do cosseno)
O teorema geral do cosseno para o lado c em falta é
c² = a² + b² − 2ab × cos γ°
e, por conseguinte,
c = a² + b² − 2ab × cos γ°
Inserindo os valores existentes
Se inserirmos os valores para a, b e gama, obtemos
c = 4² +6² − 4 × 6 × cos 70° ≈ 5,97
Solução provisória
O lado c em falta do triângulo com os lados conhecidos e um ângulo incluído conhecido é de cerca de 5,97 cm.
Agora que os comprimentos de todos os três lados são a = 4 cm, b = 6 cm e c = 5,97 cm, a "fórmula de Heron" pode ser aplicada para calcular a área.
Fórmula da área (fórmula de Heron)
A = s(s − a)(s − b)(s − c)
onde s = metade da circunferência, isto é,
s = (a + b + c) / 2
Inserindo os valores existentes
Inserindo os valores a = 4, b = 6 e c = 5,97, obtemos primeiro s com
s = (4 + 6 + 5,97) / 2 ≈ 7,98
Se inserimos s = 7,98 na fórmula de Heron, obtemos finalmente
A = 7,98 × (7,98 − 4) × (7,98 − 6) × (7,98 − 5,97)) ≈ 11,28
Solução
A área do triângulo com dois lados conhecidos e um ângulo incluído conhecido é de cerca de 11,28 cm².
5. Área de triângulos retângulos com catetos conhecidos
Se, no caso de um triângulo retângulo, os comprimentos dos dois catetos do ângulo reto forem conhecidos, então, temos, de facto, um caso especial do procedimento anterior em "Área de triângulos com dois lados conhecidos e um ângulo fechado por estes", dado que o ângulo fechado pelos dois catetos é conhecido e é de 90 graus.
Agora, podemos continuar com o cálculo tal como em 4, isto é, calcular o primeiro comprimento do lado desconhecido utilizando o teorema do cosseno e, de seguida, calcular a área do triângulo utilizando a fórmula de Heron. No entanto, um triângulo retângulo com dois catetos conhecidos permite um cálculo muito mais simples da área.
Exemplo
Neste exemplo, para calcular a área do triângulo retângulo, conhecemos os seus dois catetos a e b, onde a = 4 cm e b = 5 cm.
Fórmula da área para o triângulo retângulo
Num triângulo retângulo, os dois catetos conhecidos (aqui representados por a e b) fecham o ângulo reto. Por conseguinte, a fórmula seguinte aplica-se à área:
A = ½ × a × b
Devido ao ângulo reto entre os dois lados conhecidos, a fórmula é muito semelhante à da fórmula da área utilizada em "Área de um triângulo com um lado conhecido e uma correspondente altura h" (A = ½ × g × hg)). Isto deve-se ao facto de no triângulo retângulo a altura de a é exatamente iqual a b, ou inversamente, a altura do cateto b é exatamente a.
A fórmula da área para o triângulo retângulo pode ser ilustrada duplicando-o e colocando os dois triângulos em conjunto no seu lado oposto, a hipotenusa, de modo a formar um retângulo. Este retângulo tem a área a × b (cateto a vezes cateto b). Assim sendo, antes de duplicar, o triângulo tem exatamente metade da área, isto é ½ × a × b.
Inserindo os valores existentes
Substituindo a = 4 e b = 5 na fórmula da área para o triângulo retângulo, obtemos
A = ½ × 4 × 5 = 10
Solução
A área do triângulo retângulo é 10 cm².
6. Área de um triângulo com um lado conhecido e dois ângulos conhecidos
Para a constelação na qual qualquer lado e quaisquer dois ângulos são conhecidos para um triângulo geral, deve ser feito um pequeno trabalho preliminar para calcular a área. No exemplo seguinte, calculamos primeiro o ângulo em falta utilizando a soma dos ângulos. Com os três ângulos conhecidos, é possível determinar os dois lados restantes utilizando o teorema do seno. Assim que todos os três lados forem conhecidos, podemos continuar como em "Área de um triângulo com três lados conhecidos" e calcular a área do triângulo utilizando a fórmula de Heron.
Exemplo
Aqui tem um exemplo do cálculo da área de um triângulo geral utilizando o lado conhecido a = 4 cm e os dois ângulos α = 40 graus e β = 70 graus.
Teorema da soma do ângulo para calcular o ângulo γ em falta
Segundo o teorema da soma dos ângulos, a soma dos três ângulos interiores α, β e γ num triângulo é sempre 180 graus.
α° + β° + γ° = 180°
Quando convertida para γ° a fórmula torna-se
γ° = 180° − α° − β°
Inserindo os valores existentes
Substituindo os valores por α = 40 graus e β = 70 graus no teorema da soma dos ângulos, obtemos
γ° = 180° − 40° − 70° = 70°
Solução provisória
O ângulo em falta γ do triângulo com dois ângulos conhecidos é 70°.
Agora os dois lados restantes b e c podem ser determinados utilizando o lado e ângulo existentes. O teorema do seno é utilizado para este fim.
Teorema do seno para calcular o lado b em falta
sin β / b = sin α / a
Quando convertido para b, a fórmula é
b = a × sin β / sin α
Inserindo os valores existentes
Se substituir a, α e β no teorema seno transformado, obtemos finalmente
b = 4 × sin 70° / sin 40° = 5,85
Analogamente, o comprimento de c também pode ser calculado utilizando o teorema do seno correspondente para c.
Solução provisória
Os lados b e c em falta são b = 5,85 cm e c = 5,85 cm.
Agora que todos os três lados são conhecidos, podemos avançar como em "Área dos triângulos com três lados conhecidos" e calcular a área do triângulo utilizando a fórmula de Heron.
Fórmula da área (fórmula de Heron)
A = s(s − a)(s − b)(s − c)
onde s = metade da circunferência, isto é,
s = (a + b + c) / 2
Inserindo os valores existentes
Inserindo os valores a = 4, b = 5,85 e c = 5,85, obtemos primeiro s com
s = (4 + 5,85 + 5,85) / 2 = 7,85
Se substituirmos s = 7,85 na fórmula de Heron, obtemos finalmente
A = 7,85 × (7,85 − 4) × (7,85 − 5,85) × (7,85 − 5,85)) ≈ 10,99
Solução
A área do triângulo com um lado conhecido e dois ângulos conhecidos é cerca de 10,99 cm².
7. Área de um triângulo com dois lados conhecidos e um ângulo oposto conhecido do outro lado
Para um triângulo geral, onde dois lados e o ângulo oposto ao lado mais comprido são conhecidos, é possível calcular um triângulo único e consequentemente a área do triângulo. Para calcular a área, no entanto, tal como com a constelação de valores conhecidos em (6), alguns cálculos devem ser executados de antemão para calcular finalmente a área do triângulo:
No exemplo seguinte, os ângulos em falta são calculados primeiro. O ângulo oposto ao lado mais curto pode ser determinado com a ajuda do teorema do seno. O terceiro ângulo pode então ser determinado utilizando a soma dos ângulos. Agora o lado em falta pode ser calculado novamente utilizando o teorema do seno tendo como base os valores já calculados, antes de avançar finalmente como em "Área de um triângulo com três lados conhecidos" utilizando a fórmula de Heron para calcular a área do triângulo.
Exemplo
Aqui tem um exemplo do cálculo da área de um triângulo geral utilizando dois lados conhecidos a = 4 cm e b = 6 cm e o ângulo β = 70 graus oposto ao lado mais comprido.
O ângulo α oposto ao lado mais curto a pode ser determinado com a ajuda do seguinte teorema do seno.
Teorema do seno para calcular o ângulo α em falta
sin α / a = sin β / b
Quando convertido para α a fórmula é
α = arccos( a × sin β° / b )
Inserindo os valores existentes
Inserindo os valores para a = 4 cm, b = 6 cm e β = 70 graus, obtemos
α = arccos( 4 × sin 70° / 6 ) ≈ 38,79°
Solução intermédia
O primeiro ângulo em falta α no que diz respeito ao lado mais curto a é cerca de 38,79°.
Dado que o segundo ângulo α é agora conhecido, o terceiro ângulo em falta γ pode ser calculado utilizando o teorema da soma dos ângulos.
O teorema da soma dos ângulos para calcular o ângulo γ em falta
Segundo o teorema da soma do ângulo, a soma dos três ângulos interiores α, β e γ num triângulo é sempre 180 graus.
α° + β° + γ = 180°
Quando convertido para γ° a fórmula é
γ° = 180° − α° − β°
Inserindo os valores existentes
Substituindo os valores por α = 38,79 graus e β = 70 graus no teorema da soma do ângulo, obtemos
γ° = 180° − 38,79° − 70° = 71,21°
Solução provisória
O ângulo γ em falta do triângulo com dois ângulos conhecidos é de 71,21°.
Agora o lado c restante pode ser determinado utilizando os lados e ângulos existentes. O teorema do seno é utilizado aqui
Teorema do seno para calcular o lado c em falta
sin γ / c = sin β / b
Quando c convertido, a fórmula é
c = b × sin γ / sin β
Inserindo os valores existentes
Se substituir b, β e γ no teorema do seno transformado, obtém finalmente c = 6 × sin 71,21° / sin 70,00° = 6,04
Solução provisória
O lado c em falta é b = 6,04.
Agora que todos os três lados são conhecidos, podemos então avançar como em "Área de um triângulo com três lados conhecidos" e calcular a área do triângulo utilizando a fórmula de Heron.
Fórmula da área (Fórmula de Heron)
A = s(s − a)(s − b)(s − c)
onde s = metade da circunferência, isto é,
s = (a + b + c) / 2
Inserindo os valores existentes
Inserindo os valores a = 4, b = 5,85 e c = 5,85, obtemos primeiro s com
s = (4 + 6 + 6.04) / 2 = 8,02
Se inserimos s = 8,02 na fórmula de Heron, obtemos finalmente
A = 8,02 × (8,02 − 4) × (8,02 − 6) × (8,02 − 6,04)) ≈ 11,36
Solução
A área do triângulo com um lado conhecido e dois ângulos conhecidos é cerca de 11,36 cm².
O que os outros leitores também leram
Mais calculadoras online
Cálculo do círculo, Converter Unidades de área, Cálculo de números aleatórios, Calculadora de frações, Converter unidades de tempo, Calculadora percentual, Calculadora, Converter unidades de comprimento, Converter numeração romana
Fonte de informação
Como fonte de informação na categoria "Triângulo", utilizámos nomeadamente:
Última atualização a 20.02.2023
A página da categoria "Triângulo" foi alterada pela última vez por Michael Mühl em 20.02.2023. Além disso, a página é continuamente revista editorialmente e corresponde ao estado atual.
Alterações desta categoria "Triângulo"
- 15.01.2023: Publicação do artigo Cálculo de triângulos equiláteros.
- 14.01.2023: Publicação do artigo Área de um triângulo e Triângulos de ângulo recto.
- 12.01.2023: Publicação do tópico Calcular um triângulo juntamente com os textos correspondentes.
- Revisão editorial desta página