Aquí encontrará todas las fórmulas y numerosos ejemplos para calcular el área de los triángulos. Se consideran las áreas de los triángulos generales y especiales, como los rectángulos o los equiláteros. Con la calculadora para calcular el área del triángulo, basta con introducir las dimensiones del mismo. Además de poder visualizar el área calculada de esta manera, en los resultados de la calculadora también recibirá las derivaciones detalladas de dichos cálculos.
En la página de nuestra Calculadora de triángulos encontrará numerosos ejemplos para el cálculo de todas las características de los triángulos. O visite nuestras guías sobre los temas 'Triángulos rectángulos' y 'Triángulos equiláteros'.
Contenidos sobre el tema 'Área del triángulo'
Contenidos
- Definición de triángulo
- Nomenclaturas en los triángulos
- Área de los triángulos
- 1. Dado un lado conocido y una altura correspondiente (h)
- 2. Dados tres lados conocidos
- 3. Dado un lado conocido de un triángulo equilátero
- 4. Con dos lados conocidos y un ángulo comprendido entre ellos
- 5. Dados los catetos de un triángulo rectángulo
- 6. Con un lado y dos ángulos conocidos
- 7. Con dos lados conocidos y el ángulo opuesto al lado más largo
Definición de triángulo
Antes de abordar el cálculo del área, aquí presentamos una breve definición del triángulo y una descripción de sus términos.
Un triángulo está definido por tres puntos del plano que no se encuentran en una línea recta. Estos tres puntos son los vértices. Cada línea que une dos vértices es un lado. En el plano, el triángulo delimita una superficie.
Las propiedades importantes de un triángulo son el área, la longitud de sus tres lados, el perímetro, la relación entre sus ángulos y lados y las alturas de cada lado con respecto su vértice opuesto.
Puede calcular fácilmente el área de un triángulo y sus otras propiedades online utilizando la calculadora para calcular el área del triángulo. En la siguiente sección, también encontrará todas las opciones para calcular el área incluyendo las fórmulas y algunos ejemplos.
¿Cómo es la nomenclatura en los triángulos?
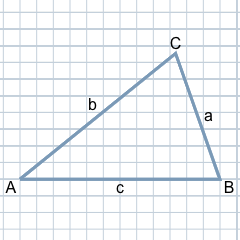
Los tres vértices de un triángulo se suelen designar con las letras mayúsculas A, B y C. Esta designación se hace en sentido contrario a las agujas del reloj y suele empezar por A en el vértice inferior izquierdo.
Los tres lados del triángulo se designan con las letras minúsculas a, b y c. El lado opuesto al vértice A se designa con la letra a, el lado b es el opuesto al vértice B y el lado c es el opuesto al vértice C.
Los tres ángulos interiores del triángulo se designan con las letras griegas α (alfa), β (beta) y γ (gamma). Están situados en los vértices correspondientes: α corresponde al vértice A, β corresponde al vértice B y γ corresponde al vértice C. La altura de un lado del triángulo corresponde a la distancia perpendicular desde el vértice opuesto a dicho lado o su prolongación. Así, la altura ha corresponde a la distancia perpendicular entre el vértice A y el lado a, es decir, el lado opuesto. Análogamente, se definen la altura de b (hb) y de c (hc).
Introducción al área del triángulo
Para calcular el área de un triángulo, basta con la longitud de un lado y su correspondiente altura. Utilizando solo estos dos valores, se puede determinar el área del triángulo. Abordaremos este caso en el siguiente apartado titulado "Área de un triángulo con un lado conocido y su altura correspondiente (h)".
Sin embargo, a menudo ocurre que no se conoce la longitud de un lado ni la altura correspondiente. En su lugar, se dan otras propiedades, como la longitud de los tres lados, u otras combinaciones de propiedades que también permiten calcular el área.
Según el primer caso mencionado, en el que se conoce un lado y su altura, veremos otras seis combinaciones de propiedades conocidas en los puntos (2) a (7) que permiten calcular el área del triángulo. Por cierto, estas combinaciones de valores conocidos, es decir, (2) a (7), no sólo sirven para calcular el área del triángulo, sino también para calcular todos los parámetros del triángulo utilizando las combinaciones. Utilizando estas combinaciones, además del área, se puede calcular el triángulo completo.
1. Área de un triángulo con un lado conocido y su altura correspondiente (h)
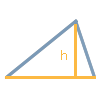Este es el "caso clásico" que suele enseñarse en primer lugar en las lecciones escolares. A partir de la longitud de un lado base (g) y la altura correspondiente (h), se puede calcular el área del triángulo con la ayuda de una sencilla fórmula. Sin embargo, estos dos datos por sí solos no son suficientes para determinar un triángulo completo de forma inequívoca, es decir, para calcular las longitudes de los demás lados y construir así el triángulo. Por otro lado, esta fórmula es la más adecuada para calcular el área.
Ejemplo
A continuación se muestra cómo calcular el área mediante un ejemplo en el que un lado a del triángulo es a = 6 cm y la altura ha = 4 cm.
Fórmula del área con un lado y su altura correspondiente conocidos
A = ½ × g × hg
donde A = área, g = longitud del lado base y h = altura del lado base
Inserción de los valores existentes
Insertando los valores a = 6 para el lado base y ha = 4 como la altura de a, obtenemos
A = ½ × 6 × 4 = 12
Solución
El área del triángulo es de 12 cm².
Por cierto, cada uno de los tres lados (a, b y c) con sus correspondientes alturas (h), pueden utilizarse para calcular el área (A).
Por supuesto, el lado base y la altura respectiva deben indicarse en la misma unidad de medida. Si, por ejemplo, el lado base se da en mm y la altura en pulgadas, primero hay que convertir una de las dos unidades antes de poder calcular el área del triángulo. Esto también se aplica a todos los cálculos de área siguientes.
2. Área de un triángulo con tres lados conocidos
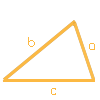Una vez obtenidos los tres lados del triángulo se pueden calcular todas sus propiedades. A continuación presentamos la fórmula de Herón para calcular el área del triángulo.
Ejemplo
Aquí le mostraremos cómo calcular el área del triángulo con un ejemplo en el que los lados están dados como a = 4 cm, b = 6 cm y c = 6 cm. .
Fórmula del área (fórmula de Herón)
A = s(s − a)(s − b)(s − c)
donde s = es la mitad del perímetro (el semiperímetro), es decir
s = (a + b + c) / 2
Inserción de los valores existentes
Insertando los valores a = 4, b = 6 y c = 6, obtenemos primero s con
s = (4 + 6 + 6) / 2 = 8
Si se sustituye s = 8 en la fórmula de Herón, se obtiene finalmente
A = 8 × (8 − 4) × (8 − 6) × (8 − 6)) ≈ 11,31
Solución
El área del triángulo con tres lados conocidos es de aproximadamente 11,31 cm².
3. Área de un triángulo equilátero con un lado conocido
Si se conoce la longitud de un lado de un triángulo equilátero, naturalmente, se conoce la longitud de los tres lados, porque los dos lados restantes tienen la misma longitud. Por tanto, tenemos un triángulo con tres lados conocidos. Ahora podríamos proceder como en "Área de un triángulo con tres lados conocidos" utilizando la fórmula de Herón. Sin embargo, esta fórmula se simplifica, dado que los tres lados tienen la misma longitud.
Ejemplo
Aquí le mostraremos cómo calcular el área utilizando un ejemplo de un triángulo equilátero cuyo lado a = 5 cm.
Fórmula del área del triángulo equilátero
A = 3 / 4 × a²
Inserción de los valores existentes
Si se inserta a = 3 en la fórmula, se obtiene
A = 3 / 4 × 5² ≈ 10,83
Solución
El área del triángulo equilátero es de unos 10,83 cm².
4. Área de un triángulo con dos lados conocidos y un ángulo comprendido entre ellos
Con dos lados conocidos y el ángulo comprendido entre ellos, se pueden calcular todas las propiedades del triángulo y, por tanto, también su área.
Por ejemplo, ahora se podría determinar primero la altura de uno de los lados conocidos (por ejemplo, para los lados conocidos a y b con su ángulo γ, la altura de b utilizando hb = a × sen γ) y luego, como se describe en "Área de un triángulo con un lado conocido y su altura correspondiente (h)", se usa la fórmula A = ½ × b × hb. En este caso, sin embargo, primero queremos calcular el tercer lado faltante utilizando el teorema del coseno y luego, como se describe en "Área de un triángulo con tres lados conocidos", utilizar la formula de Herón.
Ejemplo
El área se calcula aquí utilizando un ejemplo en el que los dos lados a = 4 cm y b = 6 cm, y el ángulo γ comprendido por a y b es de 70 grados.
Fórmula para calcular el lado faltante (teorema del coseno)
El teorema general del coseno para el lado faltante c es
c² = a² + b² − 2ab × cos γ°
entonces
c = a² + b² − 2ab × cos γ°
Inserción de los valores existentes
Si insertamos los valores de a, b y gamma, obtenemos
c = 4² +6² − 4 × 6 × cos 70° ≈ 5,97
Solución intermedia
El lado c faltante del triángulo con dos lados y su ángulo conocidos es de aproximadamente 5,97 cm.
Ahora que tenemos las longitudes de los tres lados a = 4 cm, b = 6 cm y c = 5,97 cm, podemos aplicar la "fórmula de Herón" para calcular el área.
Fórmula del área (fórmula de Herón)
A = s(s − a)(s − b)(s − c)
donde s = es la mitad del perímetro (el semiperímetro), es decir
s = (a + b + c) / 2
Inserción de los valores existentes
Insertando los valores a = 4, b = 6 y c = 5,97, obtenemos primero s con
s = (4 + 6 + 5,97) / 2 ≈ 7,98
Si insertamos s = 7,98 en la fórmula de Herón, obtenemos finalmente
A = 7,98 × (7,98 − 4) × (7,98 − 6) × (7,98 − 5,97)) ≈ 11,28
Solución
El área del triángulo con dos lados y su ángulo conocidos es de aproximadamente 11,28 cm².
5. Área de un triángulo rectángulo con los catetos conocidos
En el caso de un triángulo rectángulo, si se conocen las longitudes de los dos catetos que se encuentran en el ángulo recto, entonces tenemos, de hecho, un caso especial del procedimiento para "Área de un triángulo con dos lados conocidos y un ángulo comprendido entre ellos", ya que el ángulo comprendido por los dos catetos es conocido y es de 90 grados.
Ahora podríamos continuar con el cálculo determinando primero la longitud del lado desconocido mediante el teorema del coseno y luego calculando el área mediante la fórmula de Herón. Sin embargo, hay una forma más sencilla para calcular el área de un triángulo rectángulo con dos catetos dados.
Ejemplo
En este ejemplo, para calcular el área del triángulo rectángulo, conocemos sus dos catetos a y b, donde a = 4 cm y b = 5 cm.
Fórmula del área del triángulo rectángulo
En un triángulo rectángulo, los dos catetos conocidos (aquí a y b) delimitan el ángulo recto. Por lo tanto, se aplica la siguiente fórmula para el área
A = ½ × a × b
Dado que hay un ángulo recto entre los dos lados conocidos, la fórmula es muy similar a la fórmula del área utilizada en "Área de un triángulo con un lado conocido y su altura correspondiente (h)" (A = ½ × g × hg). Esto se debe a que en los triángulos rectángulos la altura de a es exactamente igual a la de b y viceversa.
La fórmula del área del triángulo rectángulo puede ilustrarse duplicándolo y uniendo los dos triángulos por su lado más largo, la hipotenusa, de modo que se forme un rectángulo. El área de este rectángulo es a × b (cateto a por cateto b). Por tanto, antes de duplicarlo, el triángulo tiene exactamente la mitad del área, es decir, ½ × a × b.
Inserción de los valores existentes
Sustituyendo a = 4 y b = 5 en la fórmula del área del triángulo rectángulo, obtenemos
A = ½ × 4 × 5 = 10
Solución
El área del triángulo rectángulo es de 10 cm².
6. Área de un triángulo con un lado y dos ángulos conocidos
Cuando se conocen un lado y dos ángulos cualesquiera en un triángulo general, hay que hacer un poco más de trabajo preliminar para calcular el área. En el siguiente ejemplo, primero calculamos el ángulo faltante utilizando la suma de los ángulos. Una vez que se conocen los tres ángulos, se pueden determinar los dos lados restantes mediante el teorema del seno. Tras determinar los tres lados, podemos proceder como en "Área de un triángulo con tres lados conocidos" y calcular el área del triángulo mediante la fórmula de Herón.
Ejemplo
A continuación se muestra un ejemplo del cálculo del área de un triángulo utilizando el lado dado a = 4 cm y los dos ángulos α = 40 grados y β = 70 grados.
Teorema de la suma de los ángulos para calcular el ángulo faltante γ
Según el teorema de la suma de los ángulos, la suma de los tres ángulos interiores α, β y γ de un triángulo es siempre 180 grados.
α° + β° + γ° = 180°
Cuando se convierte para γ° la fórmula es
γ° = 180° − α° − β°
Inserción de los valores existentes
Sustituyendo los valores de α = 40 grados y β = 70 grados en el teorema de la suma de los ángulos, obtenemos
γ° = 180° − 40° − 70° = 70°
Solución intermedia
El ángulo faltante γ del triángulo con dos ángulos conocidos es de 70°.
Ahora se pueden determinar los dos lados restantes b y c utilizando el lado y el ángulo existentes. Para ello se utiliza el teorema del seno.
Teorema del seno para calcular el lado b faltante
sen β / b = sen α / a
Cuando se convierte para b, la fórmula es
b = a × sen β / sen α
Inserción de los valores existentes
Si se sustituye a, α y β en el teorema del seno convertido, se obtiene finalmente
b = 4 × sen 70° / sen 40° = 5,85
De forma análoga, la longitud de c también puede calcularse utilizando el correspondiente teorema del seno para c.
Solución intermedia
Los lados b y c faltantes son b = 5,85 cm y c = 5,85 cm.
Ahora que se conocen los tres lados, podemos proceder como en "Área de un triángulo con tres lados conocidos" y calcular el área del triángulo mediante la fórmula de Herón.
Fórmula del área (fórmula de Herón)
A = s(s − a)(s − b)(s − c)
donde s = es la mitad del perímetro (el semiperímetro), es decir
s = (a + b + c) / 2
Inserción de los valores existentes
Insertando los valores a = 4, b = 5,85 y c = 5,85, obtenemos primero s con
s = (4 + 5,85 + 5,85) / 2 = 7,85
Si se sustituye s = 7,85 en la fórmula de Herón, se obtiene finalmente
A = 7,85 × (7,85 − 4) × (7,85 − 5,85) × (7,85 − 5,85)) ≈ 10,99
Solución
El área de un triángulo con un lado y dos ángulos conocidos es de aproximadamente 10,99 cm².
7. Área de un triángulo con dos lados y el ángulo opuesto al lado más largo conocidos
Para un triángulo general en el que se conocen dos lados y el ángulo opuesto al lado más largo, es posible calcular un triángulo completo y, por tanto, el área del mismo. Sin embargo, como en el caso de los valores dados en (6), hay que realizar previamente algunos cálculos para poder obtener finalmente el área del triángulo.
En el siguiente ejemplo se calculan primero los ángulos que faltan. El ángulo opuesto al lado más corto se puede determinar con la ayuda del teorema del seno. El tercer ángulo se puede determinar entonces mediante la suma de los ángulos. Ahora se puede volver a calcular el lado faltante utilizando el teorema del seno a partir de los valores ya calculados, para finalmente proceder como en "Área de un triángulo con tres lados conocidos" utilizando la fórmula de Herón.
Ejemplo
He aquí un ejemplo de cálculo del área de un triángulo general utilizando dos lados dados a = 4 cm y b = 6 cm y el ángulo β = 70 grados opuesto al lado más largo.
El ángulo α opuesto al lado más corto a se puede determinar con la ayuda del siguiente teorema del seno.
Teorema del seno para calcular el ángulo faltante α
sen α / a = sen β / b
Cuando se convierte para α la fórmula es
α = arccos( a × sen β° / b )
Inserción de los valores existentes
Insertando los valores de a = 4 cm, b = 6 cm y β = 70 grados, obtenemos
α = arccos( 4 × sen 70° / 6 ) ≈ 38,79°
Solución intermedia
El primer ángulo faltante α con respecto al lado más corto a es de unos 38,79°.
Como ya se conoce el segundo ángulo α, se puede calcular el tercer ángulo faltante γ mediante el teorema de la suma de los ángulos.
Teorema de la suma de los ángulos para calcular el ángulo faltante γ
Según el teorema de la suma de los ángulos, la suma de los tres ángulos interiores α, β y γ de un triángulo es siempre 180 grados.
α° + β° + γ = 180°
Cuando se convierte para γ° la fórmula es
γ° = 180° − α° − β°
Inserción de los valores existentes
Sustituyendo los valores de α = 38,79 grados y β = 70 grados en el teorema de la suma de los ángulos, obtenemos
γ° = 180° − 38,79° − 70° = 71,21°
Solución intermedia
El ángulo faltante γ del triángulo con dos ángulos conocidos es de 71,21°.
Ahora se puede determinar el lado restante c utilizando los lados y ángulos existentes. Para ello se utiliza el teorema del seno.
Teorema del seno para calcular el lado faltante c
sen γ / c = sen β / b
Cuando se convierte para c, la fórmula es
c = b × sen γ / sen β
Inserción de los valores existentes
Si se sustituye b, β y γ en el teorema del seno convertido, se obtiene finalmente
c = 6 × sen 71,21° / sen 70,00° = 6,04
Solución intermedia
El lado c faltante es c = 6,04.
Ahora que se conocen los tres lados, podemos proceder como en "Área de un triángulo con tres lados conocidos" y calcular el área mediante la fórmula de Herón.
Fórmula del área (fórmula de Herón)
A = s(s − a)(s − b)(s − c)
donde s = es la mitad del perímetro (el semiperímetro), es decir
s = (a + b + c) / 2
Inserción de los valores existentes
Insertando los valores a = 4, b = 5,85 y c = 5,85, obtenemos primero s con
s = (4 + 6 + 6,04) / 2 = 8,02
Si insertamos s = 8,02 en la fórmula de Herón, obtenemos finalmente
A = 8,02 × (8,02 − 4) × (8,02 − 6) × (8,02 − 6,04)) ≈ 11,36
Solución
El área del triángulo con un lado y dos ángulos conocidos es de aproximadamente 11,36 cm².
Otros usuarios han leído
Otras calculadoras online
Cálculo del círculo, Convertir unidades de superficie, Calcular fracciones, Convertir unidades de tiempo, Calculadora de porcentajes, Calculadora, Convertir unidades de longitud, Convertir a números romanos
Referencias
Como fuente de información en la categoría de "Triángulo", hemos utilizado en particular:
Última actualización
Esta página de la categoría "Triángulo" fue editada o revisada por última vez el 20.02.2023 por Michael Mühl. Corresponde al estado actual.
Cambios en esta categoría "Triángulo"
- Publicación del artículo Cálculo de triángulos equiláteros.
- Publicación del artículo sobre Área de un triángulo y Triángulos rectángulos.
- Publicación del tema Calcular triángulo junto con los textos correspondientes.
- Revisión editorial de esta página