Aire d'un triangle

Définition d'un triangle

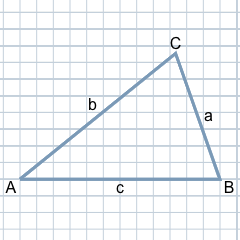
Avant de se plonger dans le calcul de l'aire d'un triangle, voici une brève définition d'un triangle et une description des termes généraux d'un triangle.

Un triangle est défini par trois points dans le plan qui ne se trouvent pas sur une ligne droite. Ces trois points sont les coins du triangle. Chaque ligne de connexion entre deux coins est un côté du triangle. Dans le plan, le triangle délimite ainsi une surface.

Les propriétés importantes d'un triangle sont son aire, la longueur de ses trois côtés, le périmètre du triangle, les angles des côtés les uns par rapport aux autres et les hauteurs de chaque côté par rapport au coin opposé. Vous pouvez facilement calculer l'aire d'un triangle et ses autres propriétés en ligne à l'aide du calculateur pour calculer l'aire d'un triangle. Dans la section suivante, vous trouverez également toutes les options de calcul de la surface, y compris les formules de calcul avec des exemples.

Comment est étiqueté un triangle ?

Les trois coins d'un triangle sont généralement étiquetés avec les lettres majuscules A, B et C. Cet étiquetage se fait dans le sens inverse des aiguilles d'une montre et commence généralement par A dans le coin inférieur gauche.

Les trois côtés d'un triangle sont désignés par les lettres minuscules a, b et c. Ici, le coin opposé latéral A est étiqueté a. En conséquence, le côté b est opposé au coin B et le côté c est opposé au coin C.

Les trois angles intérieurs d'un triangle sont nommés en utilisant les lettres grecques α (alpha), β (bêta) et γ (gamma). Ils sont situés aux coins correspondents : α appartient au coin A, β est en B et l'angle γ est en C. La hauteur d'un côté correspond à la distance perpendiculaire du point d'angle opposé à ce côté ou à son extension. Ainsi, la hauteur de a (h_a) correspond à la distance entre le coin A et le côté opposé a auquel ha est perpendiculaire. De manière analogue, la hauteur de b (h_b) et la hauteur de c (h_c) sont définies.

Introduction à l'aire des triangles

Pour calculer l'aire d'un triangle, la longueur d'un côté avec la hauteur correspondante est suffisante. En utilisant ces deux valeurs données, l'aire du triangle peut être déterminée. Nous traiterons de ce cas dans la section suivante sous "Aire d'un triangle de côté connu et de hauteur correspondante h".

Cependant, il arrive souvent que la longueur d'un côté et la hauteur correspondante ne soient pas connues. Au lieu de cela, d'autres propriétés telles que la longueur des trois côtés du triangle sont données, ou d'autres combinaisons de propriétés sont données, ce qui permet également le calcul de l'aire.

En suivant le premier cas mentionné, dans lequel un côté de base et la hauteur correspondante sont connus, nous entrons donc dans six autres combinaisons de propriétés de triangle données sous (2) à (7) sur la base desquelles l'aire du triangle peut être calculée. Par ailleurs, ces combinaisons de valeurs données, c'est-à-dire (2) à (7), conviennent non seulement pour calculer l'aire du triangle, mais également pour calculer l'aire totale du triangle à l'aide des combinaisons. En utilisant ces combinaisons, le triangle total peut être calculé en plus de la superficie.

Aire d'un triangle de côté connu et de hauteur h correspondante

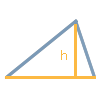C'est le "cas classique" qui est généralement enseigné en premier dans les cours scolaires. En utilisant la longueur d'un côté de base g et la hauteur correspondante h, l'aire du triangle peut être calculée à l'aide d'une formule simple. Cependant, ces deux informations ne suffisent pas à elles seules à déterminer un triangle sans ambiguïté, c'est-à-dire à calculer les longueurs des autres côtés et ainsi à construire le triangle. D'autre part, la formule suivante est la mieux adaptée pour calculer la superficie totale.

Exemple

Nous allons vous montrer ici comment calculer l'aire en utilisant un exemple où le côté a d'un triangle est donné comme a = 6 cm et la hauteur h_a = 4 cm.

Par ailleurs, chacun des trois côtés a, b et c avec leurs hauteurs correspondantes h, peut être utilisé pour calculer l'aire A.

Le côté de base respectif et la hauteur doivent bien entendu être donnés dans la même unité de mesure. Si, par exemple, le côté de base est donné en mm et la hauteur en cm, ils doivent d'abord être convertis en l'une des deux unités de mesure avant que l'aire du triangle puisse être calculée. Bien entendu, cela s'applique également à tous les autres calculs d'aire qui suivent.

2. Aire d'un triangle à trois côtés connus

Une fois que les trois côtés d'un triangle sont donnés, toutes ses propriétés peuvent également être calculées. Nous aimerions vous présenter la Formule de Héron pour calculer l'aire du triangle ici.

Example

Nous allons vous montrer ici comment calculer l'aire du triangle avec un exemple où les côtés sont donnés comme a = 4 cm, b = 6 cm et c = 6 cm.

3. Aire d'un triangle équilatéral de côté connu

Si la longueur d'un côté d'un triangle équilatéral est connue, nous connaissons naturellement la longueur des trois côtés, car les deux côtés restants ont également la même longueur. Ainsi, nous avons finalement un triangle à trois côtés connus. Nous pourrions maintenant procéder comme dans l''aire des triangles à trois côtés connus en utilisant la formule de Heron pour calculer l'aire du triangle. Cependant, cette formule est simplifiée du fait que les trois côtés sont de longueur égale.

Exemple

Nous allons vous montrer ici comment calculer l'aire en utilisant un exemple où le triangle équilatéral a une longueur de côté de a = 5 cm.

4. Aire d'un triangle avec deux côtés connus et un angle entouré par eux

Avec deux côtés connus et l'angle qui les entoure, toutes les propriétés, et donc aussi l'aire d'un triangle, peuvent être calculées.

Par exemple, on pourrait maintenant déterminer d'abord la hauteur par rapport à l'un des côtés connus (par exemple, pour les côtés a et b connus avec un angle γ inclus, la hauteur par rapport à b en utilisant hb = a × sin γ) puis, comme expliqué dans l''aire d'un triangle de côté connu et de hauteur associée h', utilisez la formule A = ½ × b × h_b.

Ici, cependant, nous voulons d'abord calculer le troisième côté manquant en utilisant le théorème du cosinus et puis, comme expliqué dans l''aire d'un triangle à trois côtés connus', utilisez la formule de Heron pour calculer l'aire du triangle avec les trois côtés connus.

Exemple

L'aire est calculée ici en utilisant un exemple où les deux côtés a = 4 cm et b = 6 cm et l'angle γ entouré par a et b est de 70 degrés.

Maintenant que les longueurs des trois côtés sont données comme a = 4 cm, b = 6 cm et c = 5,97 cm, la "formule de Héron" peut être appliquée pour calculer l'aire. Ainsi

5. Aire des triangles rectangles avec des cathètes connues

Si, dans le cas d'un triangle rectangle, les longueurs des deux cathètes se trouvant à angle droit sont connues, alors nous avons, en fait, un cas particulier de la procédure précédente dans l''aire des triangles avec deux côtés connus et un angle entouré par eux', puisque l'angle fermé par les deux cathètes est connu et est de 90 degrés.

Nous pourrions maintenant poursuivre le calcul sous 4, c'est-à-dire calculer d'abord la longueur du côté inconnu en utilisant le théorème du cosinus, puis calculer l'aire du triangle en utilisant la formule de Heron. Cependant, un triangle rectangle avec deux cathètes données permet un calcul beaucoup plus simple de l'aire.

Exemple

Dans cet exemple, pour calculer l'aire du triangle rectangle, nous connaissons ses deux cathètes a et b, où a = 4 cm et b = 5 cm.

En raison de l'angle droit entre les deux côtés connus, la formule est très similaire à la formule d'aire utilisée ici sous 'Aire d'un triangle de côté connu et de hauteur associée h' (A = ½ × g × h_g). En effet, dans un triangle rectangle, l'altitude de a est exactement b, ou inversement, l'altitude du cathète b est exactement a.

La formule de l'aire du triangle rectangle peut être illustrée en le dupliquant et en plaçant les deux triangles ensemble sur leur côté le plus long, l'hypoténuse, de manière à former un rectangle. Ce rectangle a l'aire a × b (cathète a fois cathète b). Ainsi, avant duplication, le triangle a exactement la moitié de l'aire, soit½ × a × b.

6. Aire d'un triangle avec un côté connu et deux angles connus

Pour la constellation dans laquelle un côté et deux angles quelconques sont connus pour un triangle général, un peu plus de travail préliminaire doit être effectué pour calculer l'aire : dans l'exemple suivant, nous calculons d'abord l'angle manquant en utilisant la somme des angles. Avec les trois angles connus, les deux côtés restants peuvent être déterminés à l'aide du théorème du sinus. Une fois que les trois côtés sont connus, nous pouvons procéder comme dans l''aire d'un triangle à trois côtés connus et calculez l'aire du triangle en utilisant la formule de Héron.

Exemple

Voici un exemple de calcul de l'aire d'un triangle général en utilisant le côté donné a = 4 cm et les deux angles α = 40 degrés et β = 70 degrés.

Maintenant, les deux côtés restants b et c peuvent être déterminés en utilisant le côté et l'angle existants. Le théorème du sinus est utilisé à cet effet.

De manière analogue, la longueur de c peut également être calculée en utilisant le théorème du sinus correspondant pour c.

Maintenant que les trois côtés sont connus, nous pouvons procéder comme dans l''aire d'un triangle à trois côtés connus et calculez l'aire du triangle en utilisant la formule de Héron.